Step 8 of 8: Summary
| My Name | OSLO Name |
|---|---|
| vertex | SRF |
| curvature | RADIUS |
| distance | THICKNESS |
| height | APERTURE RADIUS |
| material | GLASS |
You need to figure out how to enter all the data into a new lens table in OSLO. Basically, you just need to add four surfaces and type the numbers in.
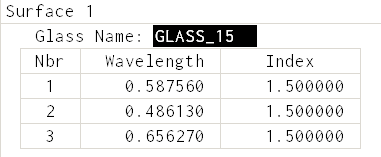
The first non-obvious thing is that I have used a "Direct" specification for the type of glass, named it "GLASS_15", and set the index of refraction for all three wavelengths to 1.5
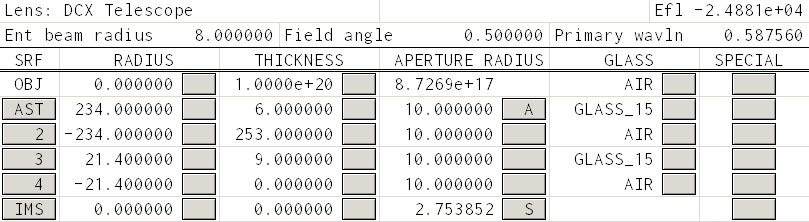
The second non-obvious thing is that I have made the radius of the beam entering the telescopes both 8mm. This is to help when we compare performance. The objective forms the limiting aperture in this system and the lenses that I chose for the PCX telescope are smaller than for the DCX telescope.
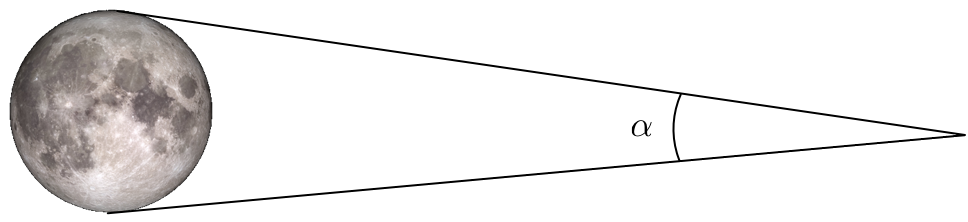
The third non-obvious thing is that I set the field angle to one-half a degree or 30 arc minutes. This is the angle $\alpha$ subtended by the moon from the earth.
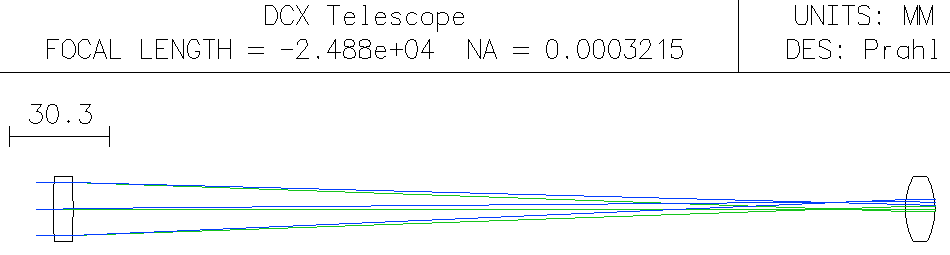
So, after putting everything together, the DCX telescope looks like
The PCX telescope looks like

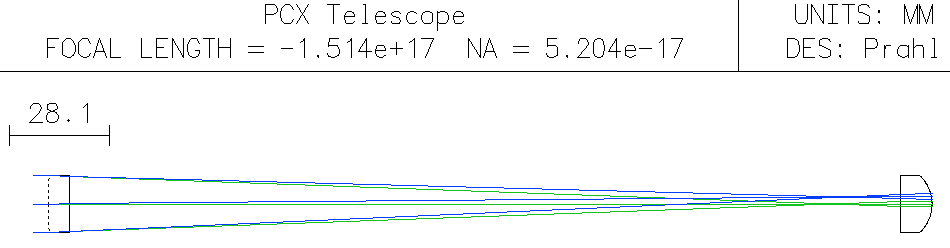
Our telescope should an afocal optical system — it does not form an image. Both the entering light rays and the exiting rays are parallel. Have we achieved this?
We have, because the effective focal length (efl in the upper right in the tables or just "focal length" in the drawing) is essentially infinite. So we did our paraxial calculations correctly.
The aperture stop (AST) is clearly the first surface. The field angle would need to be roughly 2 degrees before the eyepiece starts to block any rays. (Try it. Change the field angle to see how the light rays are affected.)

Notice is that our eyepieces are much larger than they need to be. This is why every telescope that you have probably used has a smaller eyepieces.
The diameter of the exit pupil (the diameter of the image of the aperture stop is) $$d_\mathrm{exit\,pupil}={D_\mathrm{objective}\over M} = {f_\mathrm{eyepiece} D_\mathrm{objective}\over f_\mathrm{objective}}$$ and so the exit pupil diameter will be about 2.3mm. This is a good match to the optimal pupil size for resolution of the human eye.