Step 5 of 8: Distances

If we ignore the physical thickness of the lenses, then the distances between the first and second surfaces or between the third and fourth surfaces will be zero. Furthermore, the distance from the second surface to the third surface will just be $f_o+f_e$. If you enter the following distances into OSLO, then you'll get something that looks odd.

	$d_1$	$d_2$	$d_3$	$d_4$
	mm	mm	mm	mm
DCX	0	258	0	—
PCX	0	244	0	—

Did I mix up the signs for the radius-of-curvature for the surfaces? Well, no, the drawing is correct because the distances are defined along the optical axis. As you can see, the front and back surfaces coincide on the centerline. Consequently, both biconvex and biconcave lenses will look identical in the drawing. If the distance from the front surface to the second is $t_o$, the distance from the second to the third is $f_o+f_e$, and the distance from the third to the fourth is $t_e$, then the result is as expected.

	$d_1$	$d_2$	$d_3$	$d_4$
	mm	mm	mm	mm
DCX	6	258	9	—
PCX	6	244	9	—

What about the correction for thick lenses? The focal length is the distance from the principal planes to the focus, so we can make a drawing for the DCX telescope. After a bit of squinting, you'll see that the distance from the second to the third surfaces is $(f_o-t_o/3)+(f_e-t_e/3)$.

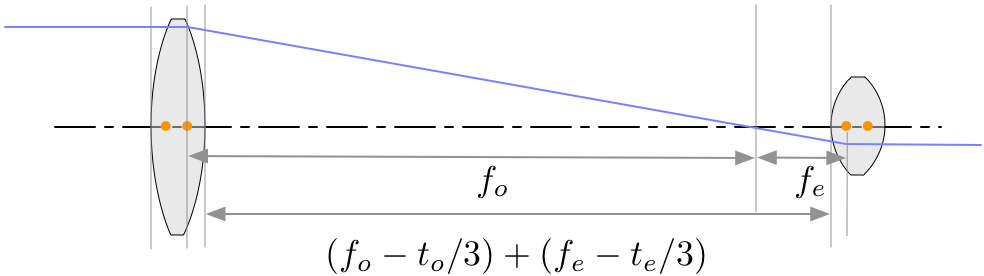
In the PCX case, things are just the same except the principal points have moved. Now the separation between the second and third surfaces will be $(f_o-2t_o/3)+(f_e-2t_e/3)$

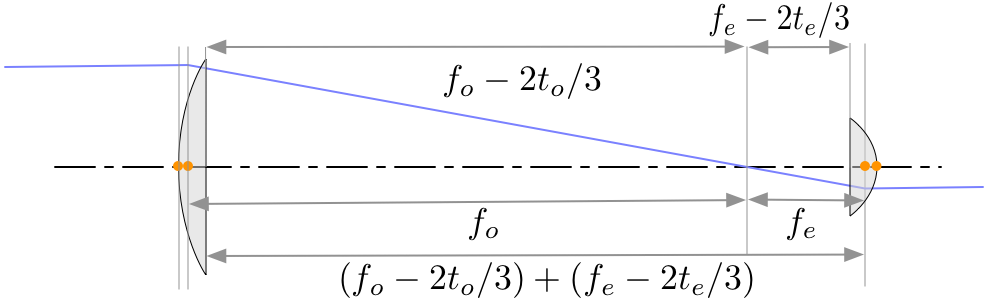
So the final thick lens paraxial design distances are

	$d_1$	$d_2$	$d_3$	$d_4$
	mm	mm	mm	mm
DCX	6	253	9	—
PCX	6	234	9	—

So which distance between the lenses should be used? Hmm, that's a good question.