Step 2 of 8: Sketch

The task is to design and build a 10X telescope. We've decided on 24mm and 240mm focal length lenses. The first thing we need to do now is to sketch the optical system. The design with double convex (DCX) surfaces is straightforward. The objective focuses the entering collimated light at a distance $f_o$. The eyepiece is at a distance $f_e$ so it re-collimates the light again

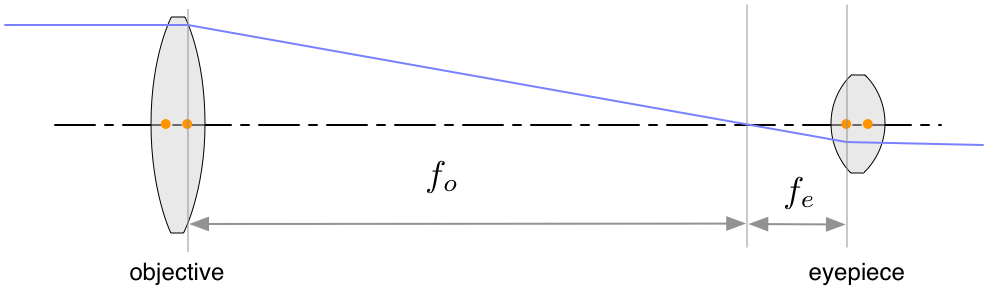
Good so far. Well, except if you worry about exactly how far apart the lenses should be located. Our lenses are not infinitely thin, so we need to use the front and back focal distances. Alternatively we can measure from the principal points of the lens. Conveniently, for a DCX lens, these points are one-third of the distance through the lens.

The one-third factor comes from our assumption that the index of refraction is $n=1.5$ and that the radius of curvature of the lens $f_\mathrm{DCX} = 2 R_\mathrm{DCX}$. If $t$ is the thickness of the lens, then the distance from a vertex to the principal point is $$\Delta = {f_\mathrm{DCX} t (n-1)\over n R_\mathrm{DCX}} = t {0.5\over 1.5}= {1\over3}t$$

The other telescope design that we'll consider is one made with two PCX lenses. The rule of thumb for orienting the lenses is to refract light evenly between the two surfaces. A bit of thought then leads to selecting the following orientation for the lenses

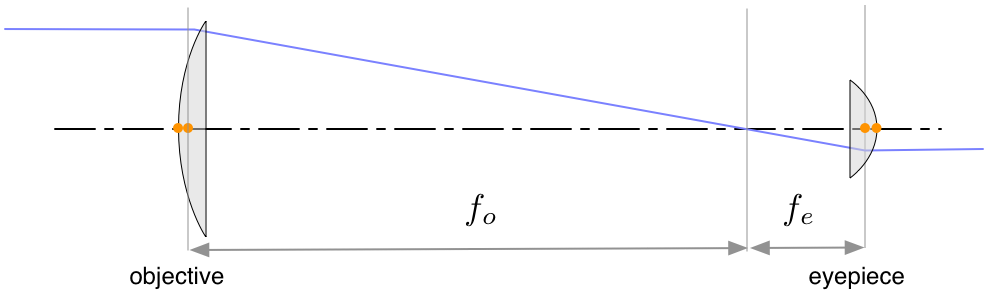
If the objective lens was reversed, then there would be no refraction of the collimated light on that surface. Consequently all the bending of light must happen on the second surface. If the lens is reversed, then some bending will take place on both surfaces which should lessen spherical aberrations. The second lens is just the opposite.

The principal points of a PCX lens fall on the curved surface and 2/3 of the distance from the flat surface.

It is worthwhile to explore why I did not use a PCX objective and a DCX eyepiece. It is also interesting to see how much worse the telescope would be if the PCX telescope did not use these orientations.