
© 1998 Steven L. Jacques, Scott A. Prahl
Oregon Graduate Institute
 |
ECE532 Biomedical Optics © 1998 Steven L. Jacques, Scott A. Prahl Oregon Graduate Institute |
Mie theory describes the scattering of light by particles. "Particles" here means an aggregation of material that constitutes a region with refractive index (np) that differs from the refractive index of its surroundings (nmed). The dipole reradiation pattern from oscillating electrons in the molecules of such particles superimpose to yield a strong net source of scattered radiation. Also, the reradiation patterns from all the dipoles do not cancel in all but the forward direction of the incident light as is true for homogneous medium, but rather interfere both constructively and destructively in a radiation pattern. Hence, particles "scatter" light in various directions with varying efficiency.
Gustav Mie in 1908 published a solution to the problem of light scattering by homogeneous spherical particles of any size. Mie's classical solution is described in terms of two parameters, nr and x:
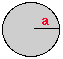
A Mie theory calculation will yield the efficiency of scattering which relates the cross-sectional area of scattering, σs [cm2], to the true geometrical cross-sectional area of the particle, A = πa2 [cm2]:
Finally, the scattering coefficient is related to the product of scatterer number density, ρs [cm-3], and the cross-sectional area of scattering, σs [cm2], (see definition of scattering coefficient):
Before using Mie theory to approximate the scattering behavior of biological tissues, let's briefly examine the Mie calculation and then illustrate the behavior of Mie scattering with some example calculations and figures