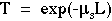© 1998 Steven L. Jacques, Scott A. Prahl
Oregon Graduate Institute
|
ECE532 Biomedical Optics © 1998 Steven L. Jacques, Scott A. Prahl Oregon Graduate Institute |
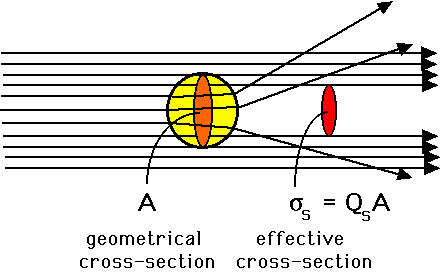
Consider a scattering particle idealized as a sphere with a
particular geometrical size. Consider that this sphere redirects
incident photons into new directions and so prevents the forward on-axis
transmission of photons, thereby casting a shadow. This process
constitutes scattering. This description is of course an oversimplified
and schematicized version of the real situation. However, it does
provide a simple concept which captures the essence of the scattering coefficient, a parameter
analogous to the absorption coefficient
discussed previously.
The size of the scattering shadow is called the effective
cross-section (σs [cm2]) and can be
smaller or larger than the geometrical size of the scattering particle
(A [cm2]), related by the proportionality constant called the
scattering efficiency Qs [dimensionless]:
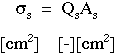
The scattering coefficient µs
[cm-1] describes a medium containing many scattering
particles at a concentration described as a volume density 
s [cm3].
The scattering coefficient is essentially the cross-sectional area per
unit volume of medium.
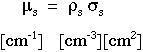
Experimentally, the units [cm-1] for µs are inverse length, such that the product µsL is dimensionless, where L [cm] is a photon's pathlength of travel through the medium. The probability of transmission T of the photon without redirection by scattering after a pathlength L is:
