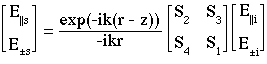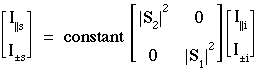|
ECE532 Biomedical Optics
© 1998
Steven L. Jacques, Scott A. Prahl
Oregon Graduate Institute |
The math of Mie scattering
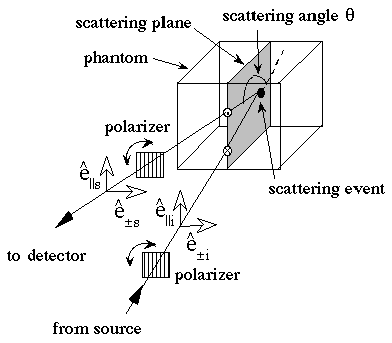
Consider a source, a spherical scattering particle, and an observer whose three positions define a plane called the scattering plane. Incident light and scattered light can be reduced to their components which are parallel or perpendicular to the scattering plane. As shown in the following figure, the parallel and perpendicular components can be experimentally selected by a linear polarization filter oriented parallel or perpendicular to the scattering plane.
The Scattering matrix describes the relationship between incident and scattered electric field components perpendicular and parallel to the scattering plane as observed in the "far-field" (ref: Bohren and Huffman):
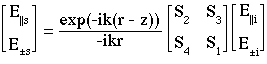
The above expression simplifies in practical experiments:
- The exponential term, -exp(-ik(r-z))/ikr, is a transport factor that depends on the distance between scatterer and observer. If one measures scattered light at a contant distance r from the scatterer, eg., as a function of angle or orientation of polarization, then the transport factor becomes a constant.
- The total field (Etot) depends on the incident field (Ei), the scattered field (Es) , and the interaction of these fields (Eint). If one observes the scattering from a position which avoids Ei, then both Ei and Eint are zero and only Es is observed.
- For "far-field" observation of Es at a distance r from a particle of diameter d such that kr >> nc2, k = 2π/
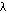 , nc = d/
, nc = d/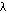 , the scattering elements S3 and S4 equal zero (see Eq. 4.75, Bohren and Huffman).
, the scattering elements S3 and S4 equal zero (see Eq. 4.75, Bohren and Huffman).
- Practical experiments measure intensity, I = <E E*> = (1/2)a2, where E = a exp(-i
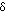 ), and a is amplitude and
), and a is amplitude and 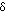 is phase of the electric field.
is phase of the electric field.
Hence for practical scattering measurements, the above equation simplifies to the following:
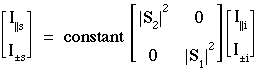
Mie theory yields two sets of descriptors of scattering:
ANGULAR SCATTERING PATTERN OF POLARIZED LIGHT
Mie theory calculates the angular dependence of the two elements, S1(θ) and S2(θ), of the Scattering matrix, from which the scattered intensities of polarized light are computed (see example). The scattering pattern is also used to calculate the anisotropy, g, of scattering by the particle.
Example of angular scattering calculation
Example of anistoropy calculation
EFFICIENCIES OF SCATTERING AND ABSORPTION
Mie theory calculates the efficiencies Qs and Qa of scattering and absorption, respectively, such that µa = QaA and µs = QsA, where A is the geometrical cross-sectional area πa2 for a sphere of radius a.
Example of Qs and µs calculation
next |
Mie theory |
Optical Properties