ECE532 Biomedical Optics © 1998 Steven L. Jacques, Scott A. Prahl Oregon Graduate Institute

Time-resolved Diffusion theory

The solution to Fick's 2nd Law of diffusion for the case of a point source of energy, U_o [units], deposited at zero time (t = 0) at the origin (r = 0) is C(r,t) [units cm^-3]:

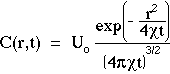
where r [cm] is the distance from the source to the point of observation, t [s] is the time of observation, and 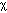[cm²/s] is the diffusivity. In the denominator, the product 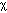t has units of [cm²] which is taken to the 3/2 power to yield units of [cm³]. The exponential in the numerator is dimensionless. The units of U_o can be the units of any extensive variable which is able to diffuse throughout a volume. Hence, C(r,t) has the proper dimensions for concentration, [units cm^-3]. The above expression for C(r,t) is a solution to Fick's 2nd law of diffusion and describes spherically symmetric diffusion from a point impulse source in a homogeneous medium with no boundaries.

For the case of optical diffusion, let F = cC and 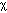= cD. Let the point source be an impulse of energy U_o [J]. The expression for fluence rate F(r,t) [W cm^-2] becomes:

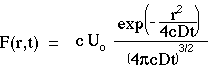
The above equation is very useful and the student of tissue optics should know this equation very well.