ECE532 Biomedical Optics © 1998 Steven L. Jacques, Scott A. Prahl Oregon Graduate Institute

Diffusion theory

Fick's 2nd law of diffusion

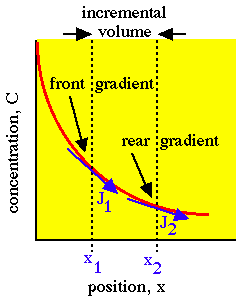
Consider diffusion at the front and rear surfaces of an incremental planar volume. Fick's 2nd law of diffusion describes the rate of accumulation (or depletion) of concentration within the volume as proportional to the local curvature of the concentration gradient. The local rule for accumulation is given by Fick's 2nd law of diffusion:

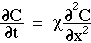
in which the accumulation, dC/dt [cm^-3 s^-1], is proportional to the diffusivity 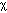[cm²/s] and the 2nd derivative (or curvature) of the concentration, 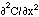[cm^-3 cm^-2] or [cm^-5]. The accumulation is positive when the curvature is positive, i.e., when the concentration gradient is more negative on the front end of the planar volume and less negative on the rear end so that more flux is driven into the volume at the front end than is driven out of the volume at the rear end.

Incremental planar volume accumulates concentration because the front gradient at x₁ drives more flux J₁ into the volume than the flux J₂ driven out of the volume by the rear gradient at x₂.

The differential equation for optical diffusion is simply Fick's 2nd law with the substitution of the product cD for the diffusivity 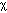and substitution of F/c for concentration C, although the 1/c factors introduced on both sides of the equation cancel: