
© 1998 Steven L. Jacques, Scott A. Prahl
Oregon Graduate Institute
 |
ECE532 Biomedical Optics © 1998 Steven L. Jacques, Scott A. Prahl Oregon Graduate Institute |
Diffusion occurs in response to a concentration gradient expressed as the change in concentration due to a change in position, 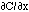 . The local rule for movement or flux J is given by Fick's 1st law of diffusion:
. The local rule for movement or flux J is given by Fick's 1st law of diffusion:
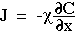
in which the flux J [cm-2 s-1] is proportional to the diffusivity 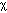 [cm2/s] and the negative gradient of concentration,
[cm2/s] and the negative gradient of concentration, 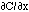 [cm-3 cm-1] or [cm-4]. The negative sign indicates that J is positive when movement is down the gradient, i.e., the negative sign cancels the negative gradient along the direction of positive flux.
[cm-3 cm-1] or [cm-4]. The negative sign indicates that J is positive when movement is down the gradient, i.e., the negative sign cancels the negative gradient along the direction of positive flux.
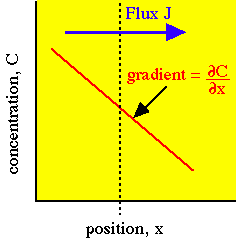
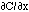 in the direction of increasing x.
in the direction of increasing x.Example: arbitrary unitsConsider a local concentration of 106 units per cm3 which drops by 10% over a distance of 1 cm. Then the gradient is -105 [units cm-4]. Assume the diffusivity is 103 [cm2/s]. Then the flux J equals: |
For light, the diffusivity is proportional to the diffusion length D [cm] and the speed of light c:
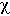 = cD
= cDwhere D = 1/(3 µs(1-g)). The units of velocity [cm/s] times the units of length [cm] yield the units of diffusivity [cm2/s]. The following example describes the local diffusion of red light in milk.
Example: optical energyConsider a local fluence rate F of 1 W/cm2 in milk (n = 1.33, µs(1-g) = 10 cm-1).
|
For optical diffusion, Fick's 1st law is expressed as the energy flux J [W cm-2] proportional to the diffusion constant D [cm] and the negative fluence gradient dF/dx:
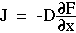
which was obtained by substituting cD for 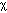 and substituting F/c for C. The factors c and 1/c cancel to yield the above equation.
and substituting F/c for C. The factors c and 1/c cancel to yield the above equation.