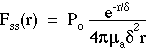ECE532 Biomedical Optics © 1998 Steven L. Jacques, Scott A. Prahl Oregon Graduate Institute

Diffusion theory

Steady-state Diffusion Theory

The time-resolved fluence rate F(r,t) [W/cm²] in response to an impulse of energy U_o [J] and the steady-state fluence rate F_ss(r) [W/cm²] in response to an isotropic point source of continuous power P_o [W] are summarized:

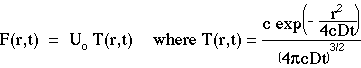
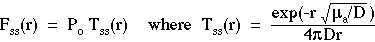
where the transport factors T(r,t) [cm^-2 s^-1] and T_ss(r) [cm^-2] have been introduced to more carefully distinguish the source, the transport, and the fluence rate.

Note on notation: In this class, we use F_ss(r) rather than F(r) to especially emphasize the steady-state fluence rate from the time-resolved fluence rate. However, F(r) should be used outside this class.

The above expression for T_ss(r) can be obtained by integrating T(r,t)exp(-µ_act) over all time to yield the total accumulated amount of photon transport to each position r. The factor exp(-µ_act) accounts for photon absorption (recall that ct = pathlength so this expression is simply Beer's law for photon survival) and causes photon concentration to approach zero as time goes to infinity. The expression for T_ss(r) is derived:

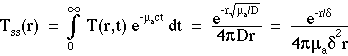
Note that the final expression above has made the substitutions:

which removes the diffusion length D and introduces the optical penetration depth δ which is the incremental distance from the source that causes F_ss(r) to decrease to 1/e its initial value. The penetration depth δ is a parameter which is very easily understood in experimental measurements and consequently has more intuitive value to some people than D which is important from the perspective of the local step size of the diffusion process. In this class we will often use the following expression for F_ss(r) when we prefer to emphasize the roles of µ_a and δ: