ECE532 Biomedical Optics © 1998 Steven L. Jacques, Scott A. Prahl Oregon Graduate Institute

Frequency-domain Diffusion theory

Isotropic point source in infinite medium

A light source may be modulated sinusoidally to yield a sinusoidally varying fluence rate distribution at a distant observation point within a medium. Such a modulated concentration will propagate in the medium and is often called a photon density wave. Consider a modulated isotropic point source of light within a homogenous turbid medium with no boundaries.

The point source S has a steady-state power S_o [W] which is modulated sinusoidally by a modulation factor M_osin(ωt), where 0 < M_o < 1:

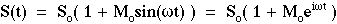
where ω = 2πf [radians/s] is the angular frequency of modulation, and the modulation frequency f is in hertz [cycles/s]. The position of observation r is located a distance r from the source. The above equation shows two ways to express S(t), one using a sine function and the other using the equivalent and well-known convention of an exponential with an imaginary exponent.

In response to this modulated source, the modulated fluence rate F(r,t) at r is described:

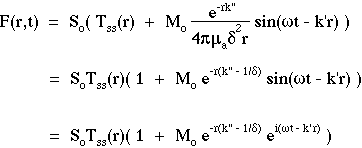
where T_ss(r) is the steady-state transport, k" is the imaginary wavenumber that describes the attenuation of the photon density wave, and k' is the real wavenumber that describes the phase lag of the observed photon density wave.

The expressions for T_ss(r), k" and k' are:

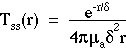
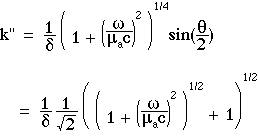
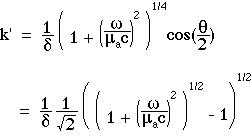
where

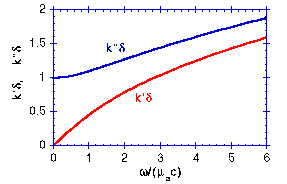
The behavior of k' and k" are shown in the following figure which plots k'δ and k"δ as functions of ω/(µ_ac):

The above expressions are equivalent to the expressions published by Schmitt et al. 1992 which in turn are equivalent to the expressions published by Fishkin et al. 1991,1993. Link to references..

At the observation point, the persistence of the source modulation is called the modulation, M, and is often described in the literature as (AC_out/DC_out)/(AC_in/DC_in) which equals:

At the observation point, the phase of the signal lags the phase of the source by an angle called the phase, φ [radians], which equals:

The ratio ω/(µ_ac) describes the number of radians of modulation cycle that occur in one mean photon lifetime. Only 1/e or 37% of photons survive after a time period of 1/(µ_ac) [s]. θ is an angle specified by the ratio ω/(µ_ac), and approaches zero for low modulation frequencies and approaches 90° at the highest modulation frequencies, ω >> µ_ac.

• At very low modulation frequencies, ω ≪ µ_ac, there is little modulation during the lifetime of a photon. Consequently, photon migration has little impact on the transport of the modulation. The value of k"δ approaches one so k" approaches 1/δ, therefore M approaches unity. The value of k' approaches zero, therefore φ approaches zero. The observed modulation of F_ss(r,t) mimics the source modulation with no loss of modulation and no phase lag. F(r,t) approaches the behavior S_oT_ss(r)(1 + M_osin(ωt)).

• At high modulation frequencies, as the modulation frequency approaches the value of µ_ac or greater, there is significant modulation during the lifetime of the photon. Consequently, the photon can diffuse during its lifetime and thereby smear the spatial resolution of the modulation. F(r,t) exhibits significant loss of modulation (M < 1) and an increased phase lag (φ > 0): F(r,t) = S_oT_ss(r)(1 + M_oMsin(ωt - k'r))