
© 1998 Steven L. Jacques, Scott A. Prahl
Oregon Graduate Institute

| ECE532 Biomedical Optics © 1998 Steven L. Jacques, Scott A. Prahl Oregon Graduate Institute |
Suppose we have a Gaussian laser beam profile of relative irradiance E(r) [mm-2] where b is the 1/e radius, i.e., E(b) = (1/e)E(0):
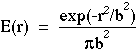
The probability density function describing the beam profile as a function of radial position r is:
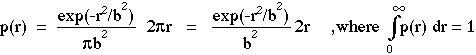
The first term is the Gaussian function exp(-r2/b2)/(![]() b2) that describes the radial dependence of the beam irradiance along one radial dimension. The second term 2
b2) that describes the radial dependence of the beam irradiance along one radial dimension. The second term 2![]() r describes the circular rings of integration over the cross-sectional plane of the beam. The product of these two terms yields the probability density function p(r) whose integration over r = 0 to infinity equals unity. The distribution function F(r) is the integral of p(r) for r = 0 to r1:
r describes the circular rings of integration over the cross-sectional plane of the beam. The product of these two terms yields the probability density function p(r) whose integration over r = 0 to infinity equals unity. The distribution function F(r) is the integral of p(r) for r = 0 to r1:
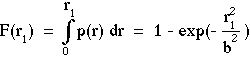
Now apply the same logic to the probability density function for a random number, p(rnd) = 1. The integral of p(rnd) for rnd = 0 to 1 equals 1, so p(rnd) is properly normalized. The distribution function F(rnd1) is the integral of p(rnd) for rnd = 0 to rnd1 which simply equals rnd1:
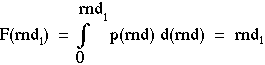
Equating the two distribution functions, F(rnd1) = F(r1), yields:
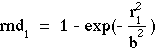
Rearrange the above equation to solve for r1 as a function of rnd1:
The above equation is the rule for sampling p(r).
The two figures below illustrate the generation of p(r) and E(r) using the above equations. The dots indicate the histograms for p(r) and E(r) created using 10,000 random numbers for rnd1. The lines indicate the analytic expressions for p(r) and E(r). The figures were generated using a MATLAB program listed here.
.gif)
p(r)
.gif)
E(r)