ECE532 Biomedical Optics © 1998 Steven L. Jacques, Scott A. Prahl Oregon Graduate Institute

Time-resolved Monte Carlo

Introduction

We are already familiar with the simple Beer's Law description of photon survival in an absorbing medium:

µ_a

absorption coefficient [cm^-1]

L

pathlength of photon travel [cm]

In a scattering medium, the photon's path is not a straight line, but Beer's law still holds. Regardless of how tortuous the path, the pathlength is given by:

L=ct

Pathlength

c

the speed of light in the medium (c = c_o/n)

t

time [s]

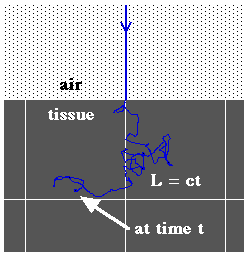
At any point in time, one can calculate the probability of photon survival by exp(-µ_aL) = exp(-µ_act).