ECE532 Biomedical Optics © 1998 Steven L. Jacques, Scott A. Prahl Oregon Graduate Institute

Mie scattering from collagen fibers

Collagen fibers are strongly scattering. For example, the dermis of skin or the sclera of the eye are tissues with high collagen fiber content. Mie theory can be used to approximate the scattering properties of collagen on two levels:

• on the macroscopic level of collagen fiber bundles.
• on the ultrastructural level of periodic striations in collagen fibrils.

macroscopic level of collagen fiber bundles

Collagen fibers vary from 0.1 µm-dia. fibrils to 8 µm-dia. fiber bundles. A study reported the distribution and concentration of collagen fiber bundle diameters in 9 post-mortem neonatal skin specimens [ref.4, Saidi et al. 1995].

• The fiber diameter (d) was 2.80 ± 0.08 µm (n = 9), i.e., (mean ± SD for n specimens), with an intraspecimen variation SD/mean = 0.43 ± 0.05.
• The fiber concentration was ρ_s = 3 x10⁶ ± 0.5 x10⁶ cm^-3. The volume fraction was f_v = πd²(1 cm)ρ_s/4 = 0.21 ± 0.10 (n = 9).

Mie theory can approximate collagen fiber scattering in dermis using the following assumptions:

• Assume n_med of the dermal ground substance is 1.350, based on a reported value for the n of corneal ground substance [ref.5].
• Assume the n_p of the collagen fiber bundles is 1.389, based on a mean dermal water content of 65.3%, W = 0.653, (see table 9.1 of ref.1): approximately, n = 1.50 - (1.50 - 1.33)W = 1.389.
• Assume one can use the cylindrical Mie theory calculation of Bohren and Huffman [appendix C in ref.6], which assumes that the incident light is oriented perpendicular to the long axis of the fiber cylinders.
• Assume that each fiber cylinder scatters light independently, ignoring any interference effects from closely spaced fibers.

The above assumptions allow calculation of µ_s(1 - g) versus wavelength for dermal collagen fiber bundles. (see "Mie" in figure below).

ultrastructural level of periodic striations in collagen fibrils

The ultrastructure of collagen fibrils presents periodic striations as was shown in the figures in our introduction to scattering. Fibrils are composed of entwined tropocollagen molecules, presenting a banded pattern of periodic striations (70-nm spacing) due to the staggered alignment of the tropocollagen molecules which each have an electron-dense head group that appears dark in the electron micrograph. The periodic fluctuations in refractive index on this ultrastructureal level appear to contribute a Mie scattering component that dominates the visible and ultraviolet wavelength ranges. Such scattering from very small structures is called the Rayleigh limit of Mie scattering, or simply "Rayleigh" scattering.

The following figure compares Mie theory for various size spheres withthe "Rayleigh" component of skin scattering seen experimentally. The "Rayleigh" behavior of skin scattering is mimiced by 50-nm-dia. spheres, n_p = 1.5, n_med = 1.35, at the volume fraction of collagen in dermis, f_v = 0.21. This assignment of the "Rayleigh" scattering to the collagen ultrastructure should be regarded as only a working hypothesis, but there is no other material in large quantity in the dermis to offer a strong source of scattering.

Combining the Mie and Rayleigh contributions for skin

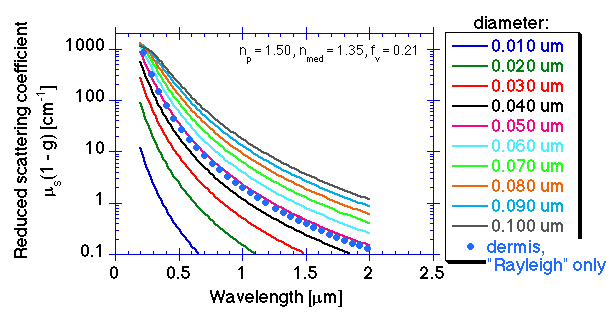
The combination of the "Mie" and "Rayleigh" contributions to scattering are shown in the following graph, along with measured skin data:

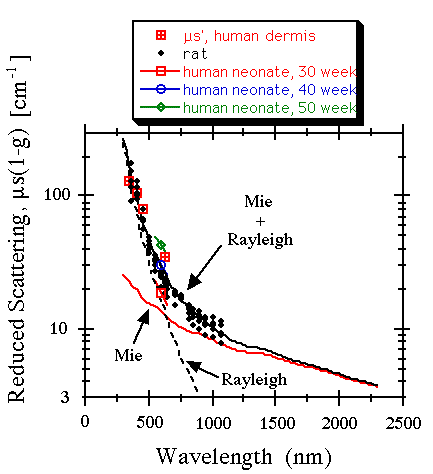
"Mie" contribution is Mie scattering from
2.8-µm-dia. cylindrical collagen fiber bundles, n_p = 1.46, n_med = 1.35, f_v = 0.21.

"Rayleigh" contribution is Mie scattering from 50-nm-dia. spheres mimicking the ultrastructure associated with the periodic striations of collagen fibrils, n_p = 1.50, n_med = 1.35, f_v = 0.21.