Example problem illustrating Monte Carlo technique: launching photons with a Gaussian laser beam distribution.

The Gaussian beam

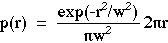
Consider the example problem of how to launch photons into a tissue so as to simulate a collimated laser beam distributed spatially as a Gaussian beam. Let the center of the beam be located at r = 0 and the distance from the center of the beam to a point of photon entry be denoted as r. Assume that the beam is a cylindrically symmetric beam around the central z-axis at r = 0. Then the probability density function for photon entry as a function of radial position r is given:

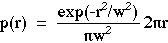
such that

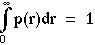
Note that we are considering a cylindrically symmetric 2D Gaussian so one must integrate the Gaussian over the incremental areas composed of annular rings of circumference (2 pi r) and radial width dr: dA = (2 pi r dr). The 2D normalization requires the normalization factor (pi w²). 1D (planar) or 3D (spherical) integrations would require different incremental areas and different normalization factors.

Setting up the Monte Carlo expression

We have learned that we wish to set up the equation

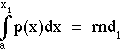
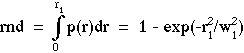
Solve the above equation for r₁ as a function of rnd:

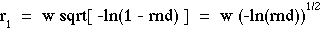
Note that -ln(1 - rnd) and -ln(rnd) will sample equivalently because rnd is a random number uniformly distributed over the interval 0 to 1, hence 1-rnd will also be a random number uniformly distributed over 0 to 1. The function sqrt[x] specifies the square root of x, which equals x^1/2.

So, our final expression is:

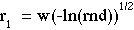
Using this expression, a set of random numbers specifies a set of values r₁ such that the histogram of r₁ values has the shape of a Gaussian beam as a function of radial position r₁ with a 1/e² radius of w.