Monte Carlo sampling of probability distributions: How to make the computer roll dice.

NewsEtc., September, 1998. Steven Jacques, Oregon Medical Laser Center

A common and well-known technique in modeling of physical processes is to use the computer for simulation. For example, we use computer simulations to mimic the movement of photons, modeled as discrete particles, through light-scattering tissues. Such modeling involves the computer drawing from a probability density function that describes the possible values of a particular parameter, such as the step size of a photon between scattering events or the angle of scattering at each scattering event. How does the computer "draw" a value? This article presents a simple discussion of the so-called "Monte Carlo" method, the name implying that the computer throws dice to draw from a probability density function in a non-biased manner.

The following three sections discuss more fully the Monte Carlo technique:

• The basic Monte Carlo technique

• Example problem illustrating Monte Carlo technique: launching photons with a Gaussian laser beam distribution.

• Verifying the expression for a Gaussian laser beam distribution.

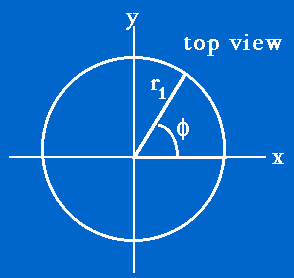
The above example of a Gaussial laser beam (w = 1 mm) is summarized by the following figure depicting how a random number rnd₁ selects a choice of radial position r₁ (mm). A choice of launch position is described by a radius r₁ and an angle as in the following figure showing a top view of photon launch down into the tissue:

The Monte Carlo method of choosing r₁ is summarized by the figure:

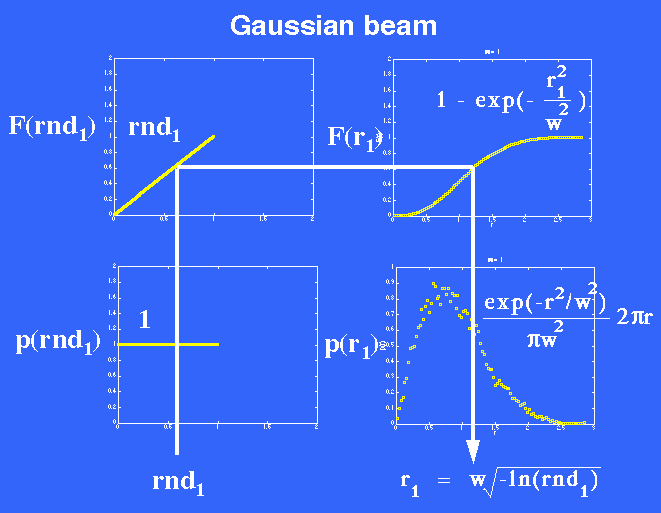
where

and

The random number rnd₁ selects a choice of radial position r₁ such that a histogram of many r₁ values will recreate the function p(r) = 2r exp(-r²)/(w²). These choices of r₁ are appropriate choices for the radial position of launching photons to approximate a Gaussian beam.

Once one has chosen the radial position r₁, one must choose the radial angle () of the photon launch point. The angle can be relative to some reference line such as the x-axis. This choice is achieved by randomly selecting an angle between 0 and 2 radians:

= 2(rnd)

then converting the r₁ and values into x, y coordinates on the tissue surface where the photon should enter the tissue:

x = r₁cos()
y = r₁sin()

For the interested reader, here are some references on the Monte Carlo method:

• E.D. Cashwell, C.J. Everett, "A Practical Manual on the Monte Carlo Method for Random Walk Problems," Pergamon Press, New York (1959).
• M.H. Kalos, P.A. Whitlock, "Monte Carlo Methods, I: Basics," John Wiley & Sons, Inc. (1986).
• I. Lux, L. Koblinger, "Monte Carlo Particle Transport Methods: Neutron and Photon Calculations," CRC Press (1991).
• A.N. Witt, "Multiple scattering in reflection nebulae I. A Monte Carlo approach," The Astrophysical J. Supp. Series 35:1-6 (1977).