OMLC
the library
NewsEtc
the blog

steve
|
ABSTRACT The penetration of light into a tissue, such as skin, depends on the wavelength of the light. Shorter wavelengths (purple, blue) penetrate less deeply than longer wavelengths (red, near-infrared). This article outlines how to estimate this penetration of light into skin. |
INTRODUCTION
Consider the uniform illumination of a skin site with white light. The skin has optical properties that depend on several tissue parameters:
| 1. Blood content, B: | The average blood content of the skin, expressed as the blood volume fraction of whole blood (150 g hemoglobin/liter). |
| 2. Tissue oxygen saturation, S: | The average oxygen saturation of hemoglobin in the arterio-venous blood vessels. |
| 3. Epidermal melanin, M: | The average volume fraction of melanosomes in the epidermis. (A 60-µm-thick epidermis is assumed, Lepi = 0.0060 cm, as a convention. The product MLepi is the actual parameter that is characterized. See Jacques & McAuliffe 1991.) |
| 2. Dermal scattering, A: | The strength of dermal scattering is characterized by the factor A, where A = 1 denotes the typical scattering spectrum observed in a variety of skin samples (human neonates, human adults, rats) that consists of both Rayleigh scattering (λ-4) from collagen ultrastructure and and Mie scattering (~λ-1) from the collagen fiber bundles. |
The optical properties used for this discussion are typical for skin:
- B = 0.002
- S = 0.60
- M = 0.10
- A = 1
These tissue parameters are used to create the following optical properties:
Absorption coefficient [cm-1]:
µa = B(Sµa.oxy + (1-S)µa.deoxy) + Wµa.water
Reduced scattering coefficient [cm-1]:
µs' = A( 8.3(λ/1000nm)-1 + 1.7(λ/1000nm)-4 )
where λ is wavelength in [nm]. The optical absorption spectra used in the calculation are
The epidermal melanin is treated as a superficial absorption filter (Tepi) that attenuates light as it enters the skin:
Tepi = exp(-MµmelLepi)
where
- M is the volume fraction of melanosomes in the epidermis, as mentioned before
- µmel is the absorption coefficient of the interior of a melanosome (REF>
- Lepi is the presumed 0.0060-cm thickness of the epidermis
Once µa and µs' are specified as functions of wavelength, the optical penetration depth of the tissue can be calculated:
&delta = sqrt(D/µa)
where
D = 1/(3(µa + µs'))
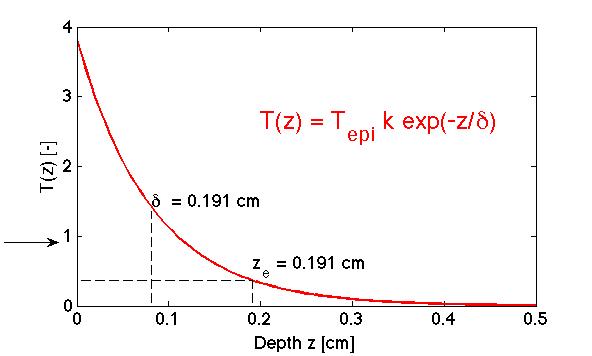
The penetration of a broad uniform beam of light into a homogeneous tissue can be summarized by the 1D transport factor T(z) [dimensionless]:
T(z) = Tepi k e-z/δ
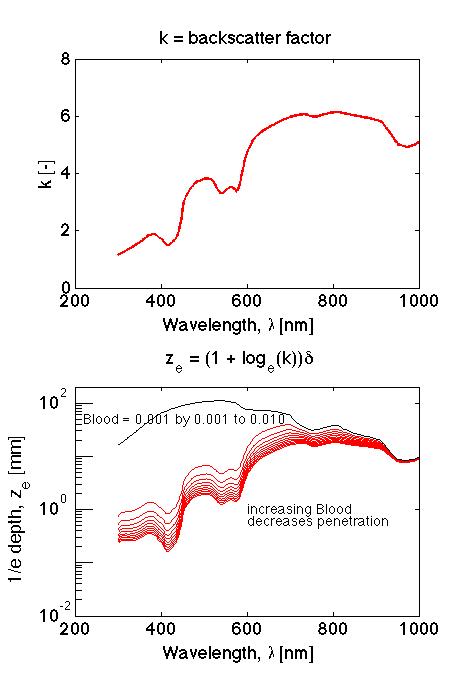
where z is the depth in the tissue and k is a backscatter factor that describes how backscattered light augments the amount of light piled up at the surface of the tissue:
k = 3 + 5.1R - 2e-9.7R
where R is the diffuse reflectance escaping the tissue. The fluence rate Φ [W/cm2] within the tissue in response to an irradiance E [W/cm2] delivered to the surface is &Phi = ET. The behavior of T is shown in Fig. 1, which would equal Φ if E = 1 W/cm2 is delivered to the tissue surface.
Fig. 1: The penetration of light into a tissue. The 1D transport factor T(z) [dimensionless] is shown. The true behavior is not correct near the surface, but is quite accurate beyond depths of ~1/µs' or 0.0230 cm or 230 µm.
Note that the depth at which the fluence rate of light (Φ) drops to 1/e or 37% of the irradiance (E) occurs at a depth ze:
ze = (1 + loge(Tepik))δ
This depth ze is a deeper than the optical penetration depth δ, which simply describes the length that causes light to drop by 1/e or 37%.
{NOTE: There is more involved in the Tepi factor than is presented here. Total internal reflection at the air/tissue interface increases the effective pathlength of photons in the pigmented epidermis. This issue is not fully developed here.}
RESULTS
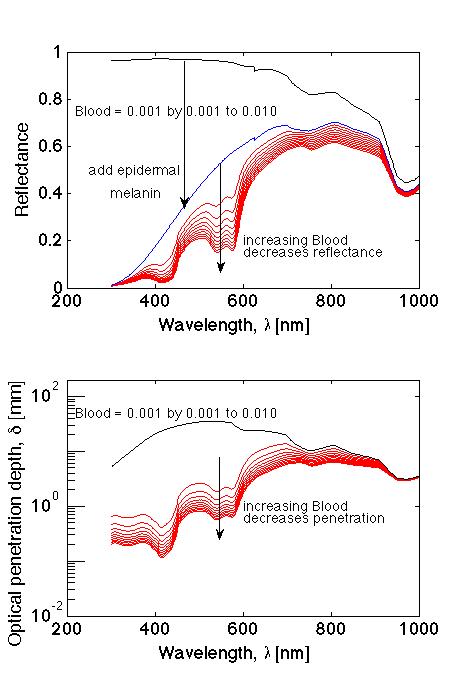
The wavelength dependence of reflectance (R) and optical penetration depth (δ) is shown in Figure 2. With no blood and no melanin, the reflectance is high over the full spectrum. Adding melanin drops the reflectance. Additionally adding blood further drops the reflectance. Similarly, adding blood decreases the optical penetration depth.
Fig. 2: (TOP) Optical reflectance versus wavelength. (BOTTOM) Optical penetration depth δ versus wavelength.
Figure 3 shows the wavelength dependence of the backscatter factor k and the 1/e depth ze.Fig. 3: (TOP) Backscatter factor k versus wavelength. (BOTTOM) 1/e depth, ze versus wavelength.
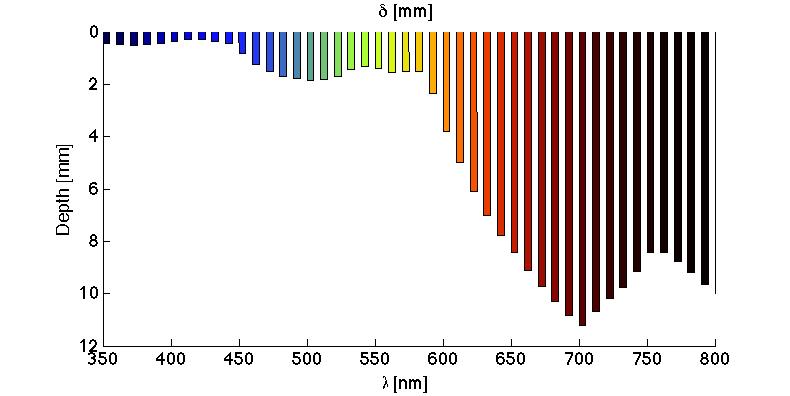
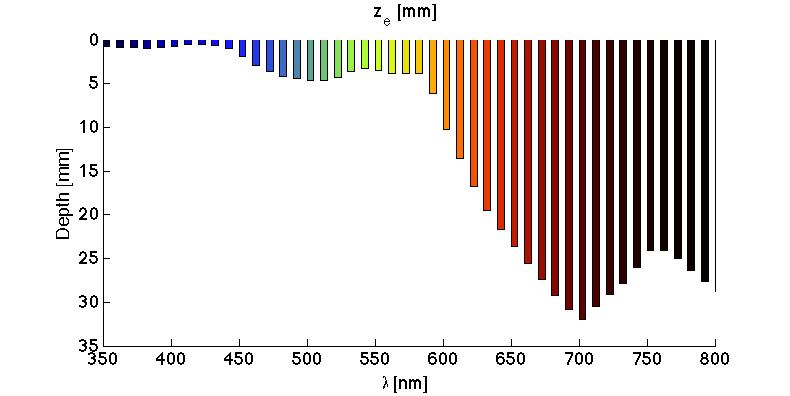
Figure 4 shows the optical penetration depth δ [mm] versus wavelength, depicted as bars extending down into skin. The penetration at very short wavelengths (<440 nm) is on the order of 0.3-0.5 mm. At middle wavelengths (440 - 600 nm), δ is about 1-2 mm. At long wavelengths (>600 nm), δ extends from 2-11 mm.
Figure 5 shows the 1/e depth, ze [mm] versus wavelength, as in FIg. 4. The ze is greater than δ by the factor (1 + loge(k)), where k is the backscatter factor.
The light penetration predicted in Figs. 4 and 5 should seem surprisingly deep to anyone familiar with delivery of light to skin. It is important to remember that this is a 1D penetration assuming an arbitrarily broad beam of uniform irradiance. The beam should be larger in diameter than 2δ. Such a broad beam is easily achieved in the short and middle wavelength ranges (<600 nm). But at longer wavelengths, the light beam is usually not sufficiently broad for 1D light transport, and one must consider the edge effects of the limited beam size (see next paragraph).
Fig. 4: The optical penetration depth δ versus wavelength.
Fig. 5: The 1/e depth ze [mm] versus wavelength.
Edge effects for finite-diameter beam
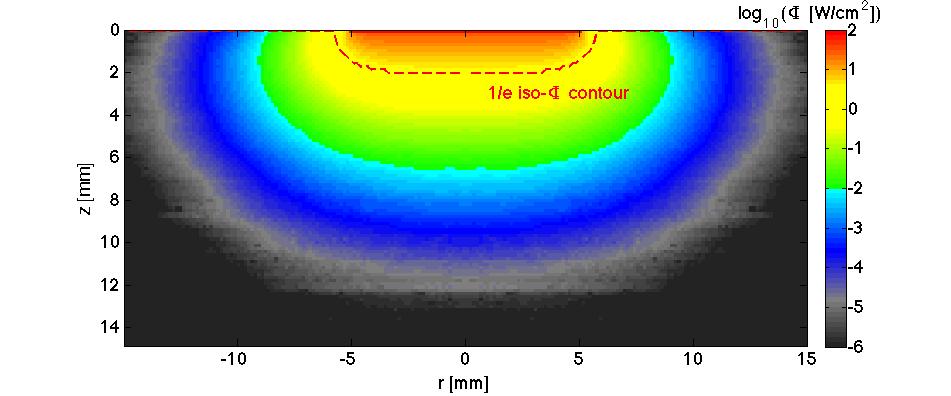
If the beam diameter is not sufficiently large, then the losses due to diffusion of light at the edges will attenuate the depth of penetration of the beam. Figure 6 illustrates a broad 6-mm-dia. beam of uniform light illuminating the skin site. The edge effects are seen to extend about 2 mm inward toward the center.
SUMMARY
The ability of light to penetrate skin depends on wavelength. Shorter wavelengths below about 450 nm will only penetrate on the scale of 200-1000 µm. Wavelengths in the mid-visible green to orange will penetrate on the scale of 1-3 mm. Wavelengths in the red to near-infrared will penetrate on the scale of 1-3 cm. Penetration decreases significantly as the blood perfusion increases.