Skin Optics
Oregon Medical Laser Center News
Jan 1998. Steven L. Jacques
In response to requests for a summary of skin optical properties,
this article presents how to choose the approximate optical coefficients
for absorption and reduced scattering of skin with variable amounts of
melanin and blood perfusion. It is merely an approximation and a
starting point for describing the skin optics of any particular
individual.
1. Epidermis
The total optical absorption coefficient (mua.epi) of the
epidermis depends on a minor baseline skin absorption and a dominant
melanin absorption due to the melanosomes in the epidermis. The
independent parameters of wavelength (nm) and volume fraction
of melanosomes (f.mel) can specify mua.epi in units of cm-1.
1.1 Baseline absorption coefficient of melaninless epidermis, mua.skinbaseline
It has been difficult to accurately distinguish the baseline
absorption coefficient values associated with melaninless epidermis and
bloodless dermis. So the baseline absorption of both epidermis and
dermis are approximated by the following mua.skinbaseline, expressed as a function of
wavelength (nm):
mua.skinbaseline = 0.244 + 85.3exp(-(nm - 154)/66.2) [cm-1]
The above expression is based on measurements of bloodless rat skin
using an integrating sphere calibrated with careful phantom measurements
(Ruiping Huang, S. Jacques, unpublished data). Iyad Saidi generated
data (450-750 nm) for in vitro neonatal skin samples using an
integrating sphere after accounting for excess absorption due to
residual hemoglobin and bilirubin in the samples
[Ref: Saidi thesis (1994)].
Those data are approximated by the expression:
mua.skinbaseline = (7.84x10^8)(nm^(-3.255)) [cm-1]
The Saidi data for neonatal skin is only a little higher in
absorption than Huang's rat data. Optically, rat skin and neonatal skin
are quite similar. The Huang data was based on a more careful
calibration of the integrating sphere apparatus and is consistent with
the rather low absorption found by many for bloodless tissues, and
extends from 350-1100 nm. We use the rat skin data as a first
approximation for mua.skinbaseline.
1.2 Absorption coefficient of a single melanosome, mua.mel
The absorption of epidermis is usually dominated by melanin
absorption in most individuals. Melanin is a polymer built by
condensation of tyrosine molecules and has a broad absorption spectrum
exhibiting stronger absorption at shorter wavelengths. Melanin is found
in the melanosome, a 1-2 um diameter membranous particle whose internal
membranes are studded with many melanin granules about 10 nm in size at
sites of melanin synthesis. On average, the interior of a melanosome
has an absorption coefficient, mua.mel, whose magnitude and
dependence on wavelength (nm) is approximated:
mua.mel = (6.6 x 10^11)(nm^(-3.33)) [cm-1]
For example,
| Ruby laser | (694 nm) | mua.mel = 230cm-1
|
| Alexandrite laser | (755 nm) | mua.mel = 170cm-1
|
| Nd:YAG laser | (1064 nm) | mua.mel = 55cm-1
|
This expression is based on various published studies of the
threshold exposure for explosive vaporization of melanosomes by pulsed
lasers at various wavelengths
[Ref: Jacques,
McAuliffe: Photochem Photobiol (1991)]. There is
considerable variation in the melanin content of melanosomes so the
above expression is only an approximation, but gives the general
magnitude and wavelength dependence of mua.mel.
1.3 Volume fraction of melanosomes in epidermis
The next question is "How many melanosomes per unit volume are in the
epidermis?" The estimated concentration ranges are expressed as the
volume fraction of the epidermis occupied by melanosomes (f.mel)
[Ref:Jacques (1996)]:
| light-skinned adults | f.mel = 1.3-6.3%
|
| moderately pigmented adults | f.mel = 11-16%
|
| darkly pigmented adults | f.mel = 18-43%
|
The above estimates are based on the wavelength dependence of the
optical density of epidermal melanin in the 650-800 nm range as
specified by skin reflectance measurements on normal vs melaninless
vitiligo skin sites and assuming a 60-um epidermal thickness and
that total photon path in the epidermis is twice the epidermal thickness
[Ref: Jacques (1995)]. Obviously, this is only an approximation and hence
a descriptive convention rather than an accurate specification.
If one wishes to specify the optical absorption of a particular skin
site on a particular individual, one can make a reflectance measurement
from that site., but the analysis goes beyond the goal of this article
...maybe later :-).
1.4 Net epidermal absorption coefficient, mua.epi
The net epidermal absorption coefficient, mua.epi, combines the baseline skin absorption and
the melanin absorption and is calculated:
mua.epi = (f.mel)(mua.mel) + (1 - f.mel)(mua.skinbaseline)
For example, a moderately pigmented adult with a
10% volume fraction of melanosomes will have absorption
coefficients as listed below and shown in Figure 1:
| | mua.skinbaseline | mua.mel | mua.epi
|
| [nm] | [cm-1] | [cm-1] | [cm-1]
|
| 694 | 0.268 | 228 | 23
|
| 755 | 0.254 | 172 | 17
|
| 1064 | 0.244 | 55 | 5.7
|
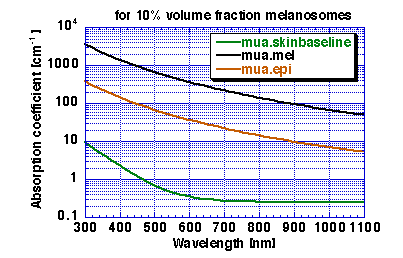
Figure 1: Absorption coefficient of epidermis with f.mel = 10%
1.5 Scattering coefficient of the epidermis.
First, consider the scattering coefficient of the epidermis,
mus.epi. Although there is surely some difference between
mus.epi and the scattering coefficient of the dermis, mus.derm,
the differences are not large. Moreover, the thinness of the epidermis
makes the details of mus.epi of minor importance for visible and
near-infrared applications involving photon diffusion. Of course,
subtle difference in mus.derm are important for devices and techniques
which primarily depend on photon interaction with the epidermis such as
measurements based on single scattering from the epidermis like elastic
backscatter, coherence backscatter, or polarized backscatter.
The second major scattering property of a tissue is its anisotropy, g, which is defined as the mean cosine
of the deflection angle due to a scattering event. Typical values of g
are in the range of 0.7-0.95 for skin tissue, and vary with wavelength.
However, for the common case of photon diffusion which involves many
scattering events, the details of mus.epi and g.epi become less
important than the lumped parameter musp.epi,
called the reduced scattering coefficient:
musp.epi = (mus.epi)(1 - g.epi)
This article will only discuss musp.epi and musp.derm.
In summary, musp.epi = musp.derm to first approximation. See section
2.4 below for discussion of musp.derm.
2.Dermis
The total optical absorption coefficient (mua.derm) of the
dermis depends on a minor baseline skin absorption and a dominant
hemoglogin absorption due to the cutaneous blood perfusion. The
independent parameters of wavelength (nm) and volume fraction
of blood (f.blood) can specify an average mua.derm in units
of cm-1. Such an average mua.derm neglects the depth dependence of the
blood which affects the optics. Remember that yellow light penetrates
skin more readily than purple and hence different wavelengths sample
blood at different depths with different efficiencies. A more careful
description will specify a depth profile for blood in the dermis.
2.1 Baseline absorption coefficient of bloodless dermis, mua.skinbaseline
As discussed in section 1.1, the baseline absorption of epidermis and
dermis are sufficiently similar that we can treat them both by the
parameter mua.skinbaseline.
2.2 Absorption coefficient of whole blood, mua.blood
The dominant absorber in the dermis is the hemoglobin of the
cutaneous blood. Figure 2 shows the absorption coefficient of whole
blood, mua.blood, defined as a having a 45% hematocrit:
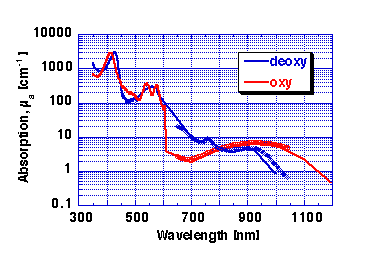
Figure 2: Absorption coefficient of whole blood (45% hematocrit).
RED = oxy-hemoglobin, BLUE = deoxy-hemoglobin.
My apologies for poor data in 600-650 nm range. Lost some data files :-(
, but will repair.
Data as symbols in 650-1042 nm range is data of Wray et al. 1998 scaled to match the whole blood data in
units of cm-1.
2.3 Absorption coefficient of dermis perfused
with blood, mua.derm
The next question is "How much blood is in the skin?" One can adopt
a descriptive convention and specify the average volume fraction of
blood, f.blood, assuming that the blood is
uniformly distributed in the skin. A typical value for this average
f.blood is 0.2%. But in reality the cutaneous blood content is
concentrated in a venous plexus about 100-200 um from the surface and
the volume fraction in this region is likely to be about 2-5%, which is
a common blood volume fraction in other well-perfused tissues. In other
parts of the dermis, the local f.blood is much lower. On average,
however, to an external observer a homogeneous blood distribution with a
low f.blood and a heterogeneous distribution with a superficially
localized high f.blood appear roughly equivalent.
Following the descriptive convention of describing an equivalent
average homogeneous f.blood, the net absorption of the dermis,
mua.derm, is calculated:
mua.derm = (f.blood)(mua.blood) + (1-f.blood)(mua.skinbaseline)
2.4 Scattering coefficient of dermis
The reduced scattering of dermis, musp.derm, combines the contributions due to Mie
scattering by the large cylindrical dermal collagen fibers and the
Rayleigh limit scattering by the small-scale structure associated
with the collagen fibers and other cellular structures. The combination
yields the observed scattering properties of dermis. Using Mie theory,
one can calculate the scattering coefficient, mus.derm, and the
anisotropy, g.derm, then calculate the musp.derm.
The epidermis with its keratin fibers appears to behave somewhat like
dermis, and musp.epi is tentatively approximated by the musp.derm.
A histological study of collagen fibers was made on 9 post-mortem
neonatal skin samples
[Ref: Saidi
(1995)]. Collagen fibers were about 2.8±0.8 um in
diameter on average with a number density of about 3.0±0.5 x 10^6
[cm^2] per cm length of fibers or 3 x 10^6 [cm^3] per unit volume. The
volume fraction of dermis filled by collagen fibers was 0.21±0.10.
Adult collagen fibers are on the higher end of this range, and the
subsequent fitting matches adult dermal scattering data [Ref: Jacques (1991)]. Using the cylindrical Mie theory outlined
in Bohren and Huffman and the number density and average size of
collagen fibers in skin, the GREEN line in Fig. 4 was calculated which
shows the contribution due to Mie scattering by collagen fibers [Ref: Jacques (1996)]. This
Mie scattering behavior can be mimicked by the expression:
musp_Mie.fibers(nm) = (2x10^5)(nm^(-1.5)) [cm-1]
Dermis also exhibits a nm^(-4) type of scattering in the Rayleigh
limit of Mie scattering by small-scale structures much smaller than the
wavelengths of UVA-Vis-NIR light. Collagen fibers show a small-scale
structure on the order of 70 nm observered in electron micrographs of
collagen fibers as striations. The staining pattern of an electron
micrograph should not be over interpreted as the pattern of refractive
index mismatch which yields light scattering. However, just as a
working hypothesis, consider that a population of light-scattering
structures comprising the collagen fiber volume fraction can be
approximated by 100-nm diameter spheres which are responsible for the
Rayleigh scattering. Using a volume fraction of 22% collagen, one can
estimate a number density of equivalent 100-nm spheres comprising the
collagen fibers. Assume these structures have a refractive index
mismatch of 1.5/1.33 for protein/water. Given the number density, size,
and refractive mismatch, one can use Mie theory for spheres to predict
the contribution to musp.derm from this small-scale structure. Since
100-nm structures are so small, the Mie Theory treament behaves as the
Rayleigh limit exhibiting the well-known nm^-(4) behavior. This
prediction yields the BLUE line of Fig. 4 [Ref: Jacques (1996)]. There
is certainly room for a more careful characterization of such postulated
small-scale scattering. However, the above crude approximate estimate
matches the magnitude and wavelength dependence of the Rayleigh
scattering component observed in dermis:
musp_Rayleigh(nm) = (2x10^12)(nm^(-4)) [cm-1]
Combining the GREEN (Mie) and BLUE (Rayleigh) lines of Fig. 4 yields
the dashed BLACK line which matches the observed RED data for dermis.
musp(nm) = musp_Rayleigh(nm) + musp_Mie.fibers(nm)
Hence, the scattering behavior of dermis is accounted for by the
combination of Mie and Rayleigh scattering primarily from collagen
fibers. The scattering behavior is dominated by Rayleigh scattering from
small-scale structure at short wavelengths below 650 nm and is dominated
by Mie scattering from fibers at longer wavelengths above 650 nm,
approximately. But the visible to near-infrared spectral region is
significantly affected by both types of scattering.
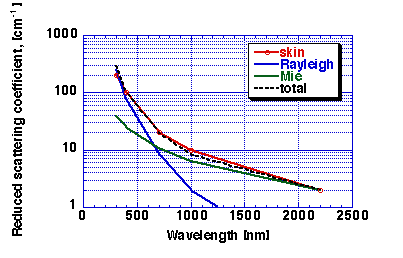
Figure 4: Reduced scattering coefficient, musp.derm, of dermis.
RED = tissue data, GREEN = Mie Theory based on collagen cylinders. BLUE
= Rayleigh limit scattering due to small-scale structure of collagen
fibers. BLACK DASHED LINE = Mie + Rayleigh, which matches tissue
data.
3. Conclusion
The optical properties of skin are
understandable. The absorption is described in terms of
melanin and hemoglobin absorption proportional to the volume
fractions of melanosomes and whole blood, with a slight baseline
skin absorption. The dermal scattering is described in terms of the
relative contributions of Mie and Rayleigh scattering due to collagen
fibers. The epidermal scattering, which is affected by its keratin
fibers, is sufficiently close to that of dermis and sufficiently thin to
not be critical, that dermal scattering can be used to describe skin
scattering in general when discussing processes or devices which rely on
photon diffusion.
Finally, adult skin optics are quite variable in the scattering
properties, the degree of melanin pigmentation, and the amount and
distribution of blood perfusion. This article has outlined only an
average skin's optical properties. Individual skin sites require
individual characterization.
January Front Page
Newsletter Contents Page