Monte Carlo: Launch a finite diameter beam

Consider launching a collimated beam of finite diameter, as opposed to launching all photons exactly at the origin as has been done so far. In this case, the position of the launch should be varied in a random manner so that a uniform spatial distribution of photon launching is achieved.

Let the beam have a radius a. The probability of launching at a radial position r is p(r):

such that

The Monte Carlo method for selecting r from p(r) using a random number, rnd, uniformly distributed between 0 and 1, inclusively, is:

Rearrange the above equation to solve for r as a function of rnd. The resulting expression will allow selection of the radial position r for launching a photon based on a random number rnd:

Photons will be launched uniformly in the x-y plane within the beam radius a. The radial magnitude r has been chosen. Now, we choose the angle phi such that the radial coordinates (r, phi) define the launch point. Let's choose phi relative to the x-axis. Then phi is specified by a second random number:

Now the positions x and y are chosen based on r and phi:

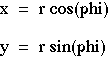
Let's choose to make a uniform circular beam with a 1-mm diameter (a = 0.05 cm). First, let's add some new variables pertinent to the launching of photons into the section of defined variables:

/* New parameters for launching photons */
double  phi;        /* angular position of launch */
double  a;          /* radius of circular beam */

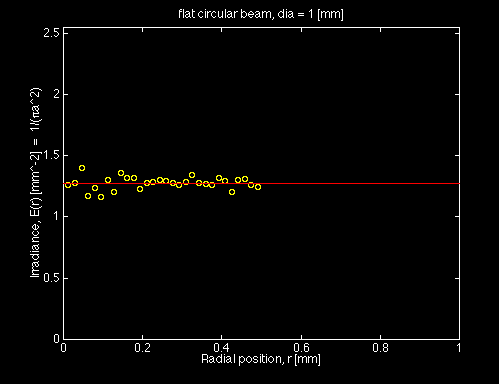
The figure below shows the random selection of position for photon launching for a uniform-irradiance circular beam. The y-axis is expressed as the irradiance E(r) [mm^-2] which equals p(r)/(2πr) = 1/(πa²). The figure was generated using a MATLAB file that launches 30,000 photons.

The following code launches photons uniformly over a circular beam of radius a using the technique described above.

/**** LAUNCH 
   Initialize photon position and trajectory.
   Implements a collimated source.
*****/
i_photon += 1;	/* increment photon count */
W = 1.0;                    /* set photon weight to one */
photon_status = ALIVE;      /* Launch an ALIVE photon */

r = a*sqrt(RandomNum);
phi = 2.0*pi*(RandomNum);

x = r*cos(phi);             /* Set photon position to origin. */
y = r*sin(phi);
z = 0;

ux = 0;   /* No x-axis trajectory */
uy = 0;   /* No y-axis trajectory */
uz = 1.0; /* All trajectory is along z-axis */