Overview¶
This presents OSLO models of a few reference eyes.
This tutorial is one of a series of OSLO tutorials that are available.
Ideas¶
Accommodated/Unaccomodated Eyes
Adding chromatic for water
Entering a simple correction for an asphere
Walker Model for the Eye¶
This follows the reference eye metrics found in Bruce H. Walker, Optical Design for Visual Systems, SPIE Tutorial Texts in Optical Engineering Volume TT45, (2000).
Walker cogently summarizes:
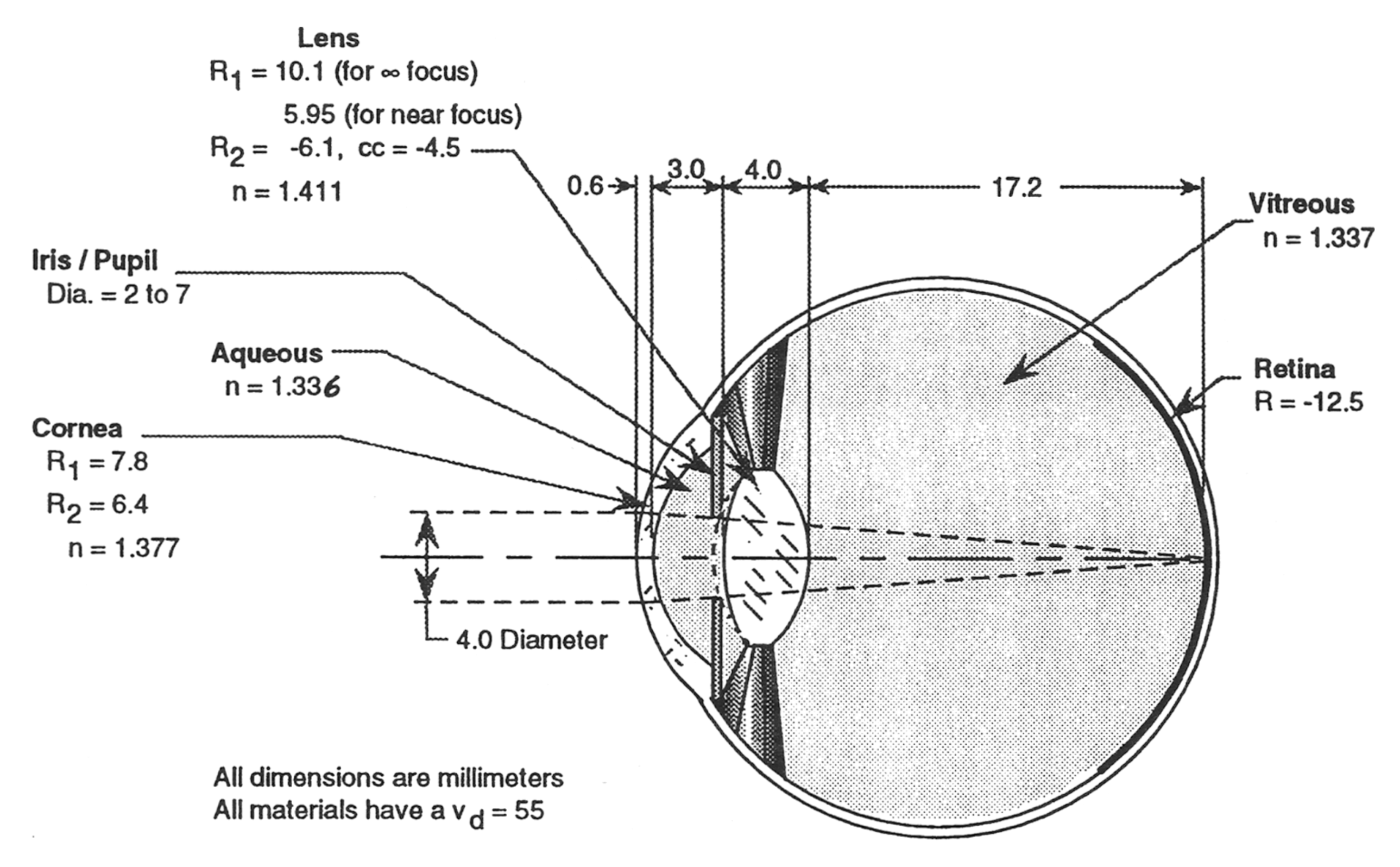
The human eye may be described (approximately) as a 1-inch-diameter water-filled sphere with a focusing lens assembly, adjustable iris, and a high-resolution sensor (the retina) at its image surface. The typical eye has a focal length of 17.3 mm, a variable f-number from f/2.5 to f/17, and adjustable focus from infinity down to 10 inches. While the full field of view of the eye is approximately 140 deg, the area of useful imagery is limited to about 90 deg. The optics of the eye are configured to reduce residual spherical aberration, while chromatic aberration remains uncorrected. The area of optimum resolution at the retina is referred to as the fovea. In most cases, when forming an image at the fovea, the optics of the eye exhibit image quality (spot size) that is from 2 to 4 times worse than the diffraction limit. Normal visual acuity is 1 arc minute, meaning that under normal conditions the eye will resolve a high-contrast, repeating pattern of equal width bars and spaces, when each element of that pattern subtends an angle of 1 arc minute to the eye. In order to be effective, the designer of optical instruments for visual applications must take into account all of the physical and optical characteristics that have been presented here.
He provides a drawing summarizing the standard eye
Accommodation¶
Accommodation describes the eye focusing on something close. For design purposes, the near point distance is the closest something can be to your eye to focus without straining. The near point distance is accepted to be 250mm.
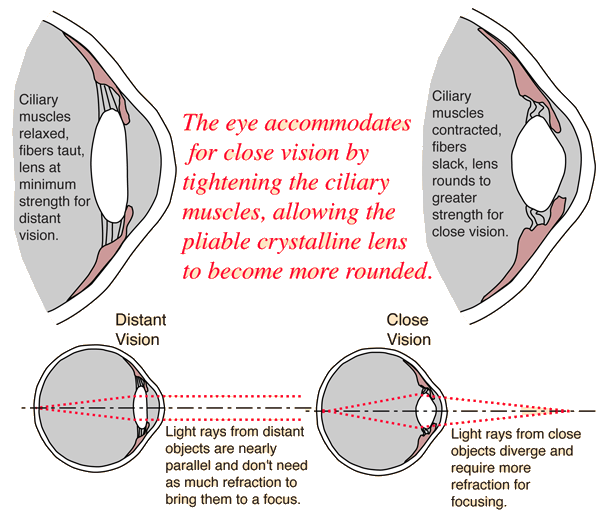
Consequently, there are two models of the eye. One for it relaxed (unaccomodated) and focused on infinity. The other is fully-accommodated and focused at the near point distance of 250mm.
Despite other physical changes, only thing that changes during accomdation is the radius of curvature of the front surface of the lens.
Unaccommodated Model¶
The unaccommodated eye has the object at infinity.
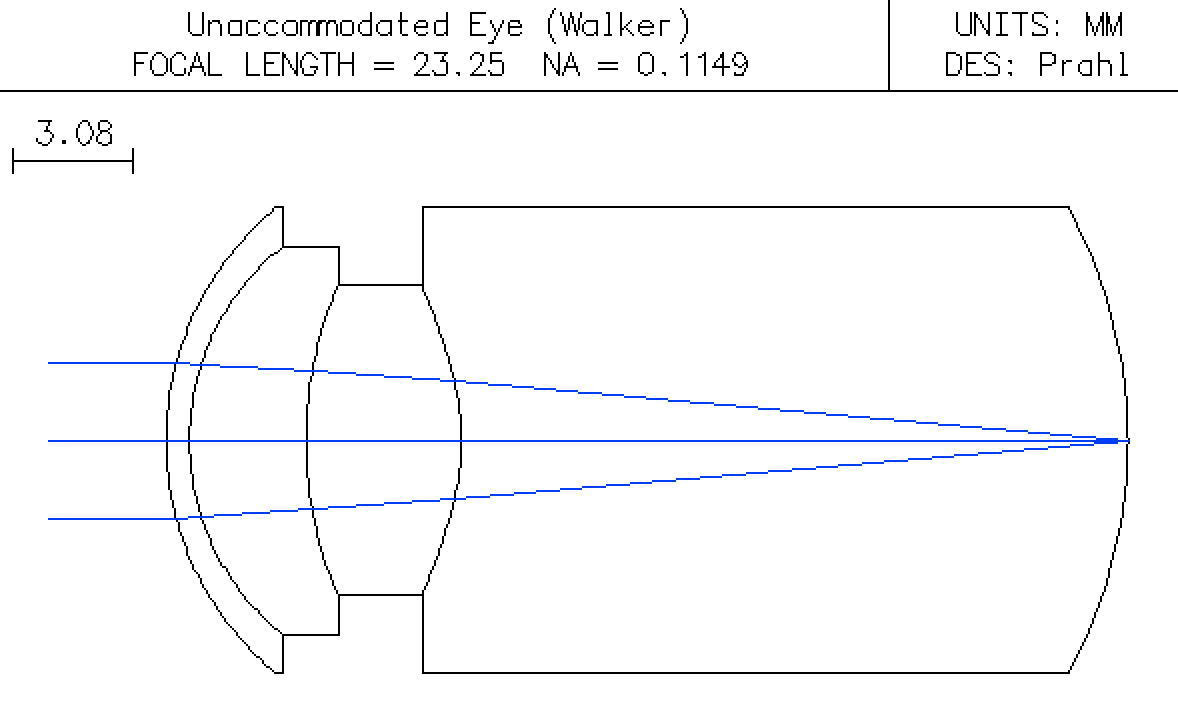
The Surface Data Window looks like
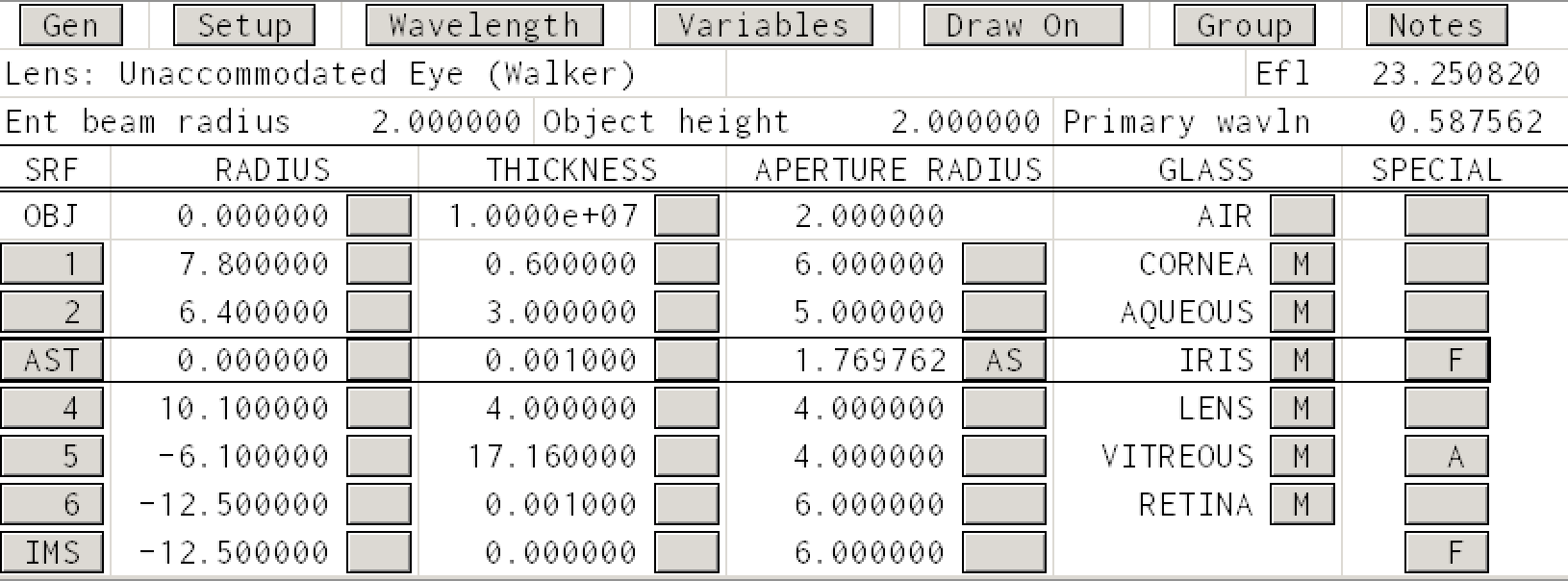
Here is the OSLO file for an unaccomodated eye
Accommodated Model¶
The accommodated eye now has the object at 250mm away.
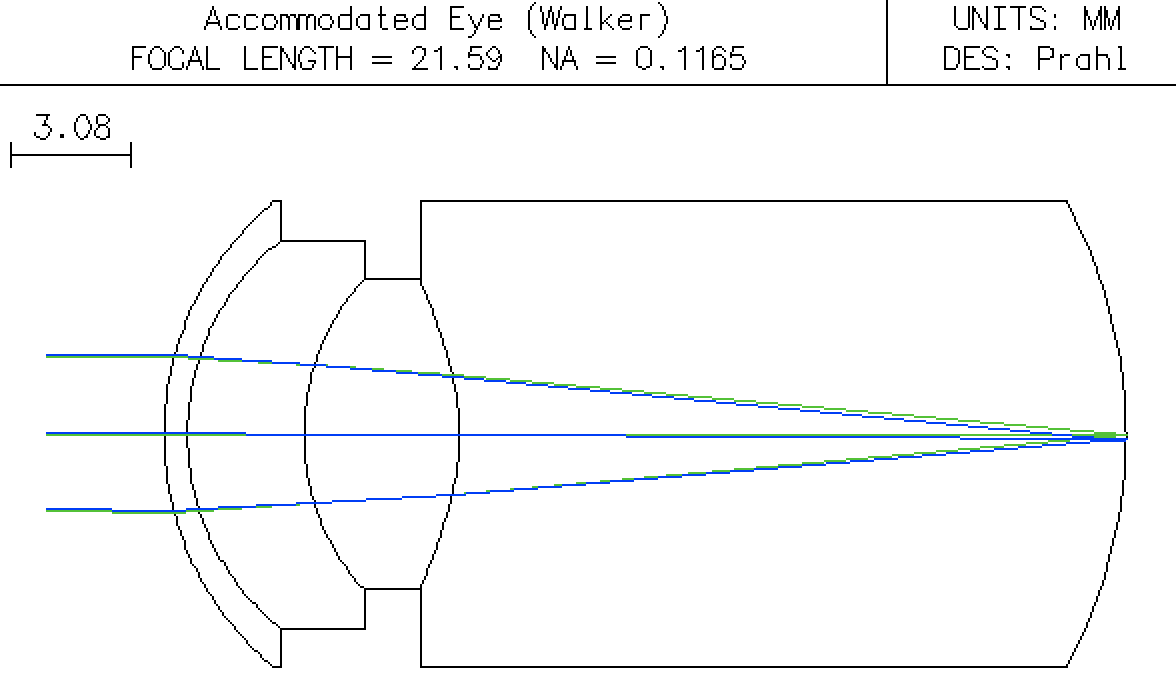
There is a slight amount of chromatic aberration seen. The Surface Data Window looks like
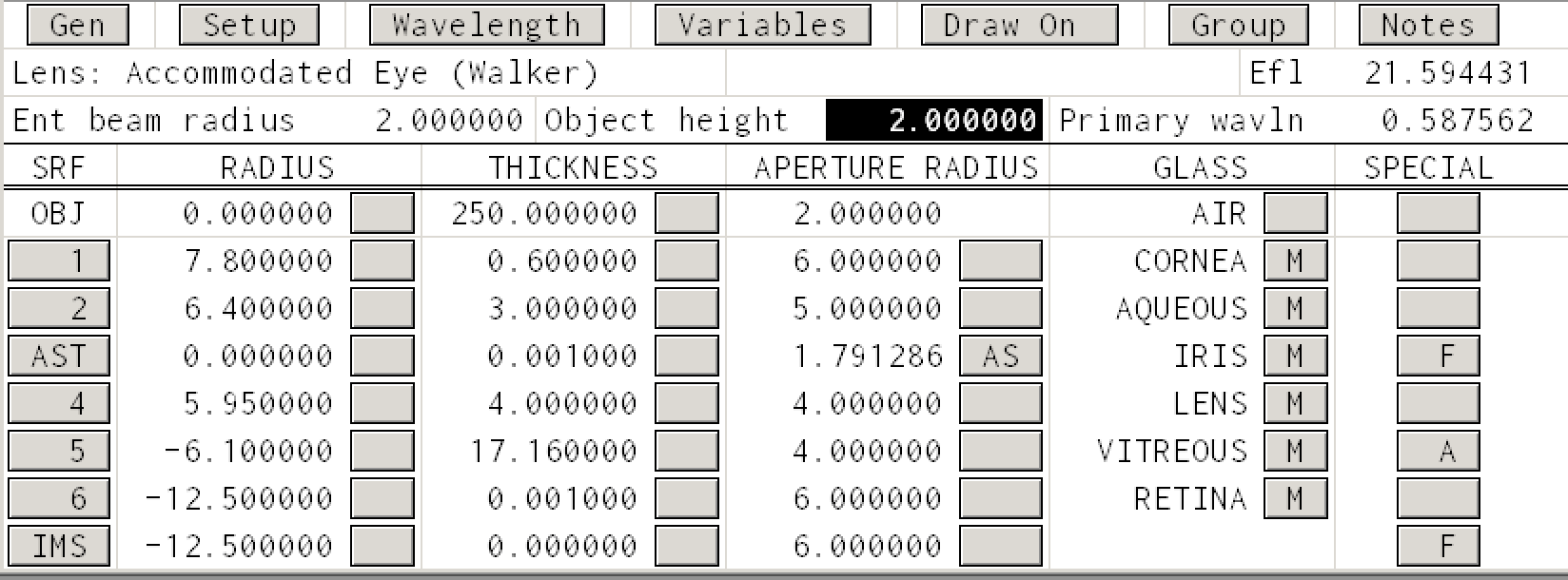
Here is the OSLO file for an accomodated eye
Indices of Refraction¶
The indices of refraction at the (green) Fraunhofer d-line at 589.3nm are
| Cornea | 1.377 |
| Aqueous | 1.336 |
| Lens | 1.411 |
| Vitreous | 1.337 |
What about the red and blue wavelengths? We use the Abbe number!
The Abbe number characterizes how the speed of light in a medium changes with wavelength. 55.81.
properties of the eye are l and the basic assumption is that the Abbe number
$$
V_d = {n_d-1\over n_F-N_c}
$$
where $n_d$, $n_F$ and $n_C$ are the refractive indices of the material at the wavelengths of the Fraunhofer d, F, and C spectral lines (589.3 nm, 486.1 nm and 656.3 nm respectively).
Walker specifies an Abbe number of $v_d=55$ that happens to be the Abbe number for water. (This is more than flint glass $v_d<50$ and closer to crown glass $v_d>50$.)
This makes sense since the eye is mostly water and its index of refraction is $n_d=1.333$ at 589.3nm. (The slight increase from water for the aqueous and vitreous humours arises from extra protein in these liquids).
The index of refraction is entered in the GLASS column for each line by clicking the button
and selecting Model...(M). It is convenient to name each component, then specify the refractive index and V-number. Once this is done, you can click the Rin button in the TW1 window to see
SRF GLASS/CATALOG RN1 RN2 RN3 VNBR TCE
0 AIR 1.000000 1.000000 1.000000 -- --
1 CORNEA 1.377000 1.380932 1.374077 55.000000 236.000000
2 AQUEOUS 1.336000 1.339504 1.333395 55.000000 236.000000
3 IRIS 1.336000 1.339504 1.333395 55.000000 236.000000
4 LENS 1.411000 1.415286 1.407813 55.000000 236.000000
5 VITREOUS 1.337000 1.340514 1.334387 55.000000 236.000000
6 RETINA 1.337000 1.340514 1.334387 55.000000 236.000000
7 IMAGE SURFACEAspherical Surface¶
You may have noticed that the back surface of the lens has a notation cc=-4.4. Walker states
A conic constant of —4.5 has been assigned to the second surface of the eyelens. This conic constant simulates the performance of the eye due to several aspheric surfaces along with variations in the index of refraction within the eyelens.
We add this correction by using the SPECIAL column. Click the button and select Polynomial Asphere (A) -> Conic/Toric to bring up the dialog box
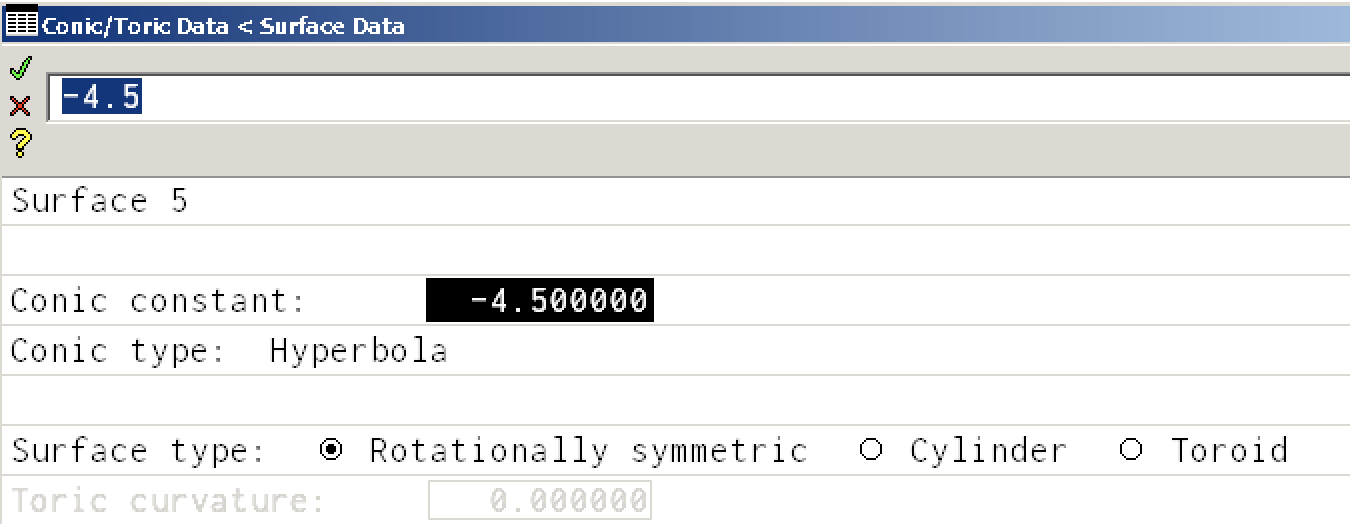
where the conic constant of -4.5 has been added.