
| ECE532 Biomedical Optics
© 1998
Steven L. Jacques, Scott A. Prahl
Oregon Graduate Institute
|
EXAMPLE: Radiance of a flashlight
Consider again our cheap flashlight example.
The flashlight projects a beam that is 200 mW over its 3-cm diameter face and projects a 10-cm circle on a wall 25 cm distant. Assume that the lamp source behaves as a point source of light located at a virtual position 10.7 cm behind the face of the flashlamp. What is the radiance at the wall?
The geometry of the problem is:
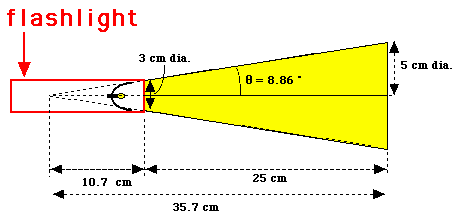
- The radiance coming out of the center of the flashlight's face will differ from the radiance exiting the periphery of the flashlight's face. Why? Because the light exiting the center is traveling in a different direction than the light exiting the periphery since the source is a point source.
- The radiant intensity is uniform over the face of the flashlight, as we already discussed, and equals I = P/Ω = 3.2 [W/sr]. But if one considers the local radiant intensity radiating from a specific location on the flashlight face into a very small solid angle along a specific direction, then I is 3.2 [W/sr] in one direction only and zero in all other directions.
- The power is uniformly distributed over our idealized flashlight. The face has an area A = π(1.5 cm)2 = 7.068 cm2.
- Therefore, the radiance L equals P/(ΩA) = I/A = (3.2 W/sr)/(7.068 cm2) = 0.453 [W/(sr cm2)] in one direction only, and L = 0 in all other directions.
- At the periphery of the flashlight face:
The angle of the intensity radiating from the periphery of the flashlight face equals tan-1((5 cm)/(35.7 cm)) = 8.86 °C. Therefore, at the periphery L = 0.453 [W/(sr cm2)] along a direction 8.86 °C off the central axis of the flashlight. L = 0 along the central axis or in any other direction.
- In the center of the flashlight face:
L = 0.453 [W/(sr cm2)] in the direction of the central axis. L = 0 in any other direction.
Next |
Radiometry


