ECE532 Biomedical Optics
© 1998 Steven L. Jacques, Scott A. Prahl
Oregon Graduate Institute

Radiant Intensity

I [W/sr]

In a given direction from a source, the radiant energy flux (or power) leaving the source, or an element of the source, in an element of solid angle containing the given direction, divided by that element of solid angle.

The power P [W] from a source that is directed into a particular direction along the center of a cone encompassing a solid angle Ω [steradians] or [sr] is called the Radiant Intensity, I [W/sr].

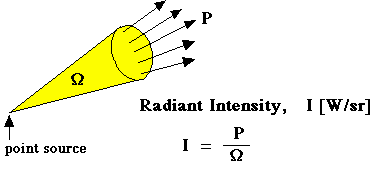
The solid angle Ω describes the size of the cone of intensity radiated by the source. Consider a sphere with radius R and a cone which intersects the sphere surface to form a circle with a radius r. For the case of a narrow cone and small cone area on the sphere surface, the following approximation holds. The area of the spot is A_circle and the surface area of the sphere is A_sphere, as shown in the figure below. There are 4π steradians over the entire surface of a sphere. So the ratio A_circle/A_sphere is the fraction of the total 4π [sr] of the sphere which is encompassed by the cone.

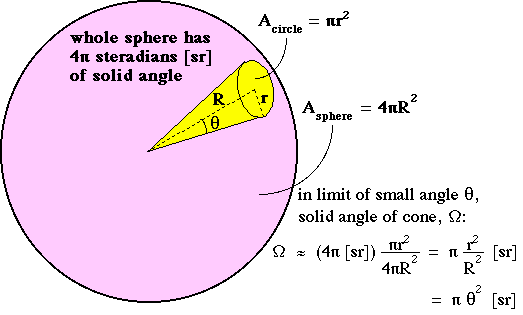
The expressions in the above figure are correct in the limit of a small solid angle. Note that r/R equals θ in the limit of small θ. The general expression for solid angle regardless of its size is:

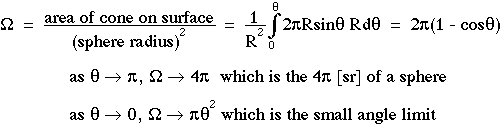
For an isotropic source of radiant power P [W] which radiates light equally in all directions, the radiant intensity is equal to P/(4π) [W/sr].

EXAMPLE: Radiant intensity of a flashlight

More generally, intensity refers to the limiting case of the ratio P/Ω for a vanishingly small cone as Ω approaches zero:

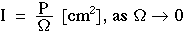
Therefore, the local radiant intensity within an irregularly shaped non-uniform-intensity region can be mapped by interrogating each portion of the region with a small cone. One is not restricted to discussing only cones.

next | Radiometry