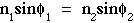ECE532 Biomedical Optics © 1998 Steven L. Jacques, Scott A. Prahl Oregon Graduate Institute

Collection by an optical fiber

An optical fiber can guide rays of light due to multiple internal reflectance at the interface between the central fiber core (refractive index n₁) and the surrounding cladding (refractive index n₂). (More about REFRACTIVE INDEX in the next class.)

Consider an optical fiber collecting light from its surroundings, as shown in the following figure. The fiber is a central core of glass surrounding by a polymer cladding and is collecting light from the LEFT in the air.

A ray of light enters the glass core of the fiber at its open end (on the left) at an angle θ₁ relative to the fiber axis. The angle of incidence is bent by refraction at the air/glass interface into a new angle θ₂ which is oriented more closely to the fiber axis. (More about REFRACTION next class.) The ray obliquely (angle φ₁) strikes the glass/polymer interface of the core/cladding surface and is internally reflected . (More about INTERNAL REFLECTANCE next class.) The ray continues to be multiply internally reflected as it propagates down the fiber to the RIGHT. Rays that enter the fiber from outside the cone of collection will not be successfully internally reflected and will escape the fiber and not propagate.

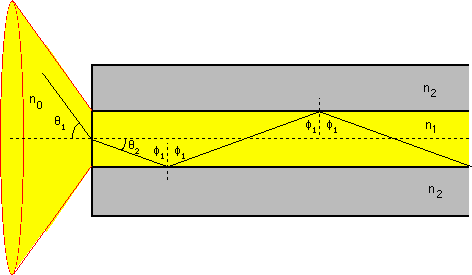
The situation with the optical fiber is equivalent to the aperture with restricted solid angle of collection which was discussed earlier. Only power flowing into the fiber within the acceptance angle of the fiber will be internally reflected within the fiber and successfully transmitted down the fiber to some detection system. In general, the acceptance angle θ_a depends on the values of n₀, n₁ and n₂ according to the expression:

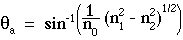
EXAMPLE: Assume typical fiber conditions:

• the medium surrounding the fiber is air with a refractive index n₀ = 1.0
• the core is glass, n₁ = 1.50
• the cladding is a polymer, n₂ = 1.47.
• the acceptance angle is:
  θ_a = sin^-1( (1/1.0)(1.50² - 1.47²)^1/2 ) = 17.4°
• The solid angle of collection is: Ω = π(r/R)²   (see previous figure and equation)
  
  = π(tan(θ_a))² = 0.984 [sr]

Brief introduction to Snell's Law

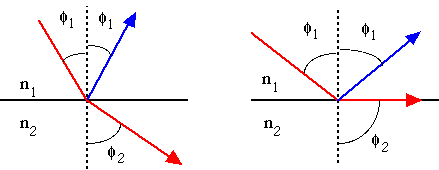
Snell's Law describes the angle of transmission (φ₂) of a light ray in response to an angle of incidence (φ₁) at an interface between two media with different refractive indices. The angle of reflectance is equal in magnitude to the incident angle.

• The LEFT figure below shows the basic rule. A ray of light is incident at angle φ₁ relative to the normal to the interface. The ray transmitted into medium 2 from medium 1 is turned into a new angle φ₂. In this example, n₂ < n₁.
• The RIGHT figure shows the special case of incidence at the critical angle called φ_c at which the transmitted ray is aligned with the interface. There is zero transmission into medium 2. At any angle φ₁ > φ_c, there is no transmission and the ray is totally internally reflected into medium 1 at an angle of magnitude φ₁ opposite the incident angle.