Optical Elastography
Sean J. Kirkpatrick
Department of Biomaterials and Biomechanics
Oregon Health Sciences University
Portland, OR 97201
USA
Abstract
A maximum likelihood estimator for quantifying shifts in speckle patterns resulting from an applied stress to biological tissue is described. The estimator is then applied to calculating the strains and instantaneous strain rates in chicken skeletal muscle subjected to a dynamic acoustic (2 Hz) sinusoidal loading.
1. Introduction
Optical elastography, as defined here, is the field of study that aims to use coherent light techniques to evaluate the mechanical behavior of materials. Of immediate interest is the use of laser speckle methods for investigating the mechanical behavior of biological tissues. The use of laser speckle techniques for the mechanical characterization of materials is well known in the non-destructive evaluation community.1-4 One particular application is to infer strain by monitoring the motion of the speckle pattern that results from coherently illuminating a stressed object. Typically a reference image of the speckle pattern is acquired before deformation of the object. Motion (with respect to this reference image) of subsequent speckle patterns, which occurs when the object is stressed, is used to infer the resulting strain. A problem experienced in using this technique for measurements of hydrated tissues is the rapid decorrelation of the speckle patterns.5 Thus, application of speckle techniques to assessment of strain in biological tissues often relies upon rapid sampling of the speckle patterns and the use of processing algorithms that are aimed at inferring strain rates rather than absolute strains.
The goal of optical elastography is to noninvasively, or minimally invasively, quantify meaningful mechanical constants of tissues in a manner that provides clinically relevant information. It is well known that many disease processes, such as tumors of the breast and prostate, manifest themselves as stiff, hard nodules relative to the surrounding tissue. This feature frequently allows for their detection through manual palpation. However, soft tissue palpation is not only qualitative, but also highly subjective. Furthermore, it provides information on a relatively large spatial scale. Thus the ability to detect small tumors by palpation is limited. Manual palpation is also limited to those areas of the body which are accessible to touch. Optical elastography offers the potential for increased spatial resolution (i.e. smaller lesions may be detected) and better strain resolution (low-contrast elastic modulus distributions may be visualized) than other elastographic methods, such as vibration amplitude sonoelastography,6 vibration phase gradient sonoelastography,6 elastography,7 spectral tissue strain measurement,8 and various methods employing MRI data.9. Strain resolution on the order of single microstrain has been evaluated in biological tissue optically.10 However, this increased spatial and strain resolution is gained at the cost of decreased probing depth as coherent optical methods are limited to the outer few millimeters of tissue. Furthermore, most optical elastography methods are limited in that only relatively small areas or volumes of tissues may be probed at any one time. Nevertheless, optical methods can still be useful in the early detection of neoplastic changes because many of these early changes occur in the mucosa and submucosa of the affected organs. Subsurface skin tumors present themselves as objects with distinct mechanical properties relative to the surrounding normal tissue. The displacement of fibrillar papillary dermis by the softer, cellular mass of a growing melanoma is one such example of this. Optical elastographic techniques may provide a means by which to probe these masses to determine their state of progression and thereby help to determine a proper means of disease management. Other skin afflictions, such as psoriasis and icthyosis, also present as localized tissue areas with distinct mechanical properties that can be delineated optically.
The conventional strategy behind most one- and two-dimensional speckle techniques that are aimed at measuring surface displacements is to compute the correlation between a reference and displaced (sample) speckle patterns. This approach is straightforward and has been used successfully in processing data from speckle strain gauges.11-13 This approach, however, is subject to errors and certain limitations for biomedical diagnostics. For example, if the test is subject to vibrations, there will always be some question as to the validity of the reference exposure. Furthermore, if the speckle shifts are substantial, the speckle pattern will decorrelate from the reference and a new reference must be chosen. This can lead to compounding of errors.
However, since the goal of these conventional approaches is simply to quantify a lateral shift in a "noisy" signal, a number of other data collection and data analysis options present themselves. One data collection scheme that has proven to be very useful for evaluating strains in biological tissues begins with the fundamental concept of the laser speckle strain gauge as described by Yamaguchi11-13. The configuration is appropriate for either objective or subjective laser speckle.The scheme is based upon observing translating laser speckle with a linear array CCD camera through an observation angle, q o, as the specimen is sequentially illuminated through two equal, but opposite illumination angles, " q s by a collimated laser beam (Fig. 1).
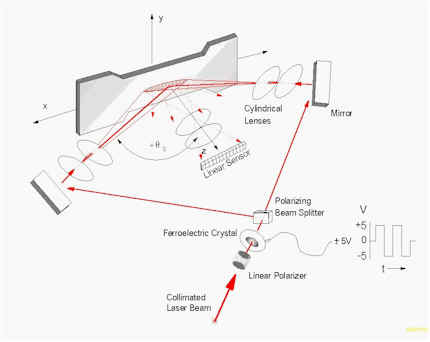
Figure 1. Optical arrangement for collecting speckle data.
Alternatively, a two detector, single beam configuration is also possible.13-15 Due to the fast decorrelation of the observed speckle patterns as a result of random movements within the tissues (water, blood, etc.), the switching of the illumination angle and subsequent triggering of the CCD array must be rapid enough to acquire at least several records with minimal decorrelation between subsequent exposures. Typically, the switching must be on the order of 50 Hz.10,16 This frequency is beyond the range of most mechanical shutters so electro-optical devices, such as ferroelectric crystals (FLC), in combination with polarizing beam splitters have been used in the past.10,16 In this case, the FLC acts as a binary, switchable half-wave plate and the beam is thus transmitted through or reflected by the polarizing beam splitter, depending upon the polarization of the light exiting the FLC.
Using a physical optics approach, Yamaguchi11 has shown that for an object undergoing strain the speckle motion observed through q o for illumination angle q s is given by
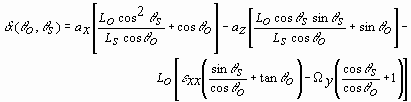 ,
(1)
,
(1)
where ax is an in-plane motion, az is an out-of-plane motion, e xx is the linear strain in the plane of the detector and laser beams (ultimately, the desired term), W y is a rotation about the axis perpendicular to the measurement plane, Ls is the radius of the illuminating wavefront (i.e., the source distance), and Lo is the observation distance. By using the illustrated configuration where q o = 0° , by using collimated beams (Ls * ), and by subtracting the speckle motions as observed from the two equal, but opposite illumination angles, a relation describing the differential speckle motion, d A, can be derived from Eq. (1):
![]() .
(2)
.
(2)
It can be seen, then, that the in-plane strain term can readily be isolated. Had the complementary configuration (2 cameras, 1 laser beam) been employed, Eq. (2) would have taken the form
![]() (3)
(3)
and the desired strain term could only be isolated if the term containing az was made negligible to the strain term. This can be accomplished through a proper choice of Lo and q o.
The goal of this strain measurement concept is to determine the shift in a speckle pattern resulting from an applied load. Towards this end, the one-dimensional records are stacked into what is termed a "stacked-speckle history."14,15 Stacked speckle histories are time series of one-dimensional views of the speckle patterns combined in a spatio-temporal array such that the spatial dimension (camera pixel) is along the abscissa and the temporal axis is the ordinate. In the configuration shown in Fig. 1, two stacked speckle histories are generated, one for each q s. Figure 2 is a gray-scale display of one such stacked speckle history taken from an object undergoing a slow linear strain. The figure shows a sequence of 200 one-dimensional

Figure 2. Stacked speckle history of a sample undergoing a linear strain. Time is given by the y-axis and space is given by the x-axis.
speckle patterns stacked one atop another. The desired information, that is, the shift of the speckle pattern is reflected in the tilt of the structure.
Processing of these stacked speckle data has been
accomplished using the transform method.10,15 The method has been
adequately described in the literature and therefore will be only summarized
here. In the transform method of processing stacked speckle histories, the
speckle histories are visually inspected and matching sets of 10-30 records
from each history that display minimal decorrelation, or for some other
experiment-driven reason, are selected for analysis. These records are
transformed into the frequency domain using a fast Fourier (FFT) algorithm in
the spatial direction and an autoregressive (AR) spectral estimator (modified
covariance, 3-5 poles) in the temporal direction. Alternatively a 2-dimensional
FFT may be employed. The result of this operation is a pair of
"images" in the frequency domain consisting of a bright band of energy
oriented perpendicular to the tilt in the stacked speckle histories. The slopes,
m1 and m2, respectively, have the dimensions
of length/time and quantify the time rate of speckle pattern shift, ![]() .
Thus, by taking the time derivative of Eq. (2), and rearranging to isolate the
desired strain term, we get a simple expression for directly estimating the time
rate of in-plane strain,
.
Thus, by taking the time derivative of Eq. (2), and rearranging to isolate the
desired strain term, we get a simple expression for directly estimating the time
rate of in-plane strain, ![]() ("
confidence intervals):
("
confidence intervals):
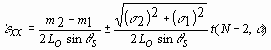 ,
(4)
,
(4)
where the subscripts are associated with the positive and negative illumination angles, s is the standard deviation about each slope, respectively, and t is the critical value of the Student's t-distribution with N-2 degrees of freedom at a probability level of a . Absolute strains can be determined by an integration over the time course of the experiment.
2. Methods
There are numerous alternative approaches that can be employed for determining speckle movement. One such alternative is a parametric approach, a maximum likelihood estimator. Parametric estimators incorporate a priori knowledge of the experiment (as opposed to non-parametric estimators, such as cross-correlation approaches, which do not incorporate a priori knowledge). The objective, of course in using a such model-based estimators is to gain a degree of sensitivity. By making use of information that is known about the conditions of the measurement, non-physical outcomes can be eliminated. While this often results in greater resolution, this increased resolution sometimes comes with a price. Typically non-parametric approaches are more robust. Because the parametric approaches implicitly eliminate estimates that are "non-physical", when data are encountered that are less than ideal, these estimators sometimes break down. One of the fundamental assumptions in this (and other) approaches is that the two speckle records are simple translates of one another. With analogy to one of the basic tools of the theory of propagation through atmospheric turbulence, Taylor's frozen turbulence hypothesis,17 this may be called the "frozen speckle" model. The maximum likelihood estimator described below arises from a minimum mean square error techniques when it is assumed that the noise in the speckle signal is Gaussian.
2.1. A Maximum Likelihood Speckle Shift Estimator
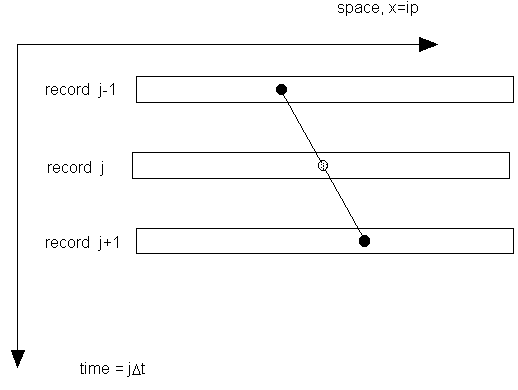
It is assumed that, over a time on the order of a couple sequential exposures of the camera, the structure of the speckle pattern is fixed. The only change with time is its lateral motion (Fig. 3).
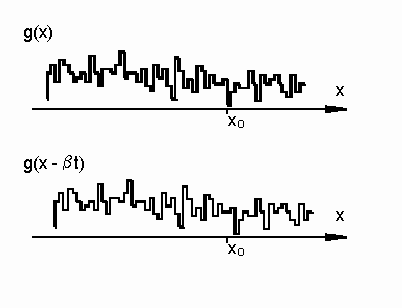
Figure 3. Illustration of shifting frozen speckle pattern.
Thus the speckle motion can be modeled as
![]() ,
(5)
,
(5)
where the subscript i denotes the pixel (spatial dimension) and the subscript j represents the record (temporal dimension). Assuming that the shift, dx is small compared to a pixel, Eq. (5) can be approximated as
![]() .
(6)
.
(6)
This is simply the first two terms of the Taylor series expansion for g. To introduce a degree of symmetry into the problem, the two speckle records on either side of the record of interest are inspected (Fig. 4),
![]() .
(7)
.
(7)
Figure 4. Central differencing technique.
The dx that minimizes the error is then determined,
![]() .
(8)
.
(8)
where the sum is over all pixels in the array. The dx that brings these two records into registration is thus sought. Equation (8) may be solved numerically by making use of a gradient search algorithm.18 If however, we make use of the approximation in Eq. (6) (small speckle motions), then differentiation with respect to dx and rearranging yields the formula
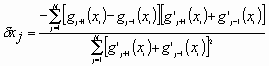 .
(9)
.
(9)
The term in the first square bracket in the numerator is simply the first central difference approximation19 to the derivative;
![]() .
(10)
.
(10)
The spatial derivatives may be approximated similarly:
![]() ;
(11)
;
(11)
.
Note that the shift parameter, dx, is the time rate at which the speckle pattern shifts; units are pixels/record.
Although the means by which the estimate for dx was arrived at was quite specific, this estimation approach is more general than it would seem. For instance, the term approximating the 1st central difference for the estimate of the temporal derivative arose because the speckle records on either side of the record of interest where chosen for inspection. We could just as easily have included additional records and weighting their contributions appropriately to estimate higher order approximations to the derivative. For example, instead of using the weights
![]() ,
(12)
,
(12)
we could use20
![]() .
(13)
.
(13)
In this case, the formulation for the mean square error would be
![]() ,
(14)
,
(14)
the temporal derivative term of Eq. (13) would be
![]() ,
(15)
,
(15)
and the term involving the spatial derivatives would be
![]() .
(16)
.
(16)
Note that this is simply the weighted average,
![]() ,
(17)
,
(17)
of the terms on either side of the record of interest. Further, these higher order operators for the derivative can be used to estimate the spatial derivatives:
![]() .
(18)
.
(18)
These higher order approximations to the derivative have somewhat better noise characteristics.19 This improvement, however, comes at the expense of reduced temporal resolution. Nevertheless, by making use of these higher order approximations, the processing can be tailored to the demands of the experiment.
Up to this point, no specific assumptions about the statistics of the speckle pattern or associated noise have been made. The only a priori knowledge that was introduced is that the speckle shift is small with respect to the pixel size. If the assumption is now made that the measured speckle signal comprises a deterministic speckle signal(!) plus noise, the measured signal can be modeled as
![]() ,
(19)
,
(19)
where n is a zero-mean noise signal. If we calculate the central difference about the jth record, we get
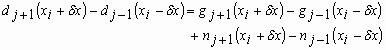 .
(20)
.
(20)
It is assumed that the sequential speckle patterns are constant mean. Further it is assumed that the noise is statistically independent Gaussian with zero mean and constant variance. As a result the noise probability density function can be written as
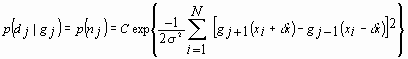 ,
(21)
,
(21)
where C is a constant. Equation (21) is commonly referred to as the likelihood function.21 To choose the dx that maximizes this likelihood we set
![]() .
(22)
.
(22)
Carrying out this calculation leads to the formula in Eq. (9). It is straightforward to show that this is an unbiased estimate of the speckle pattern shift and that the variance of the estimate attains the Cramer-Rao lower bound.22
For any of the differential speckle measurement techniques, whether it be single detector and two laser beams or single laser beam and two detectors, one arrives at a pair of stacked speckle histories. These histories display the time rate of movement of the individual speckles whether they are subjective or objective. The relationship between these speckle motions and the strain undergone by the test specimen is dictated by the actual measurement configuration. As an example, consider the configuration shown in Fig. 1. If dx1 and dx2 represent the speckle motions derived from the two speckle histories (one for laser beam #1 and the other for laser beam #2), then the object strain in the plane of the detector and beams is given by
![]() ,
(23)
,
(23)
where Lo is the effective object difference and q s is the illumination angle. For objective speckle, the effective object distance is the physical distance between the object and the detector focal plane. In the case of subjective speckle, it is the misfocus distance. For the complementary configuration of one normally incident laser beam and two cameras, the corresponding relationship is
![]() ,
(24)
,
(24)
where q o is the observation angle. Note that these are the same results as Eqs. (2-4).
2.2. Acousto-optic Elastography
In this section of the paper, we present a method, acousto-optic elastography (AOE), which employs the above described maximum likelihood speckle shift estimator for evaluating the strain response of chicken skeletal muscle to an applied acoustic load. In AOE, a contact electroacoustic transducer is placed adjacent to a region of interest (ROI) of the tissue and is driven with a sinusoidal waveform at low frequency. The ROI is then sequentially illuminated with a low power laser from two equal, but opposite illumination angles, " q s. The backscattered speckle pattern is imaged by a linear array CCD camera equipped with a telecentric lens as in Fig. 1. The system is intentionally misfocused by a distance Lo in order to observe any speckle translation due to the acoustic loading. A perfectly focused imaging system would produce a "boiling" speckle pattern, as opposed to a translating pattern and our goal was to track the translating speckle pattern as a function of the imposed acoustic stress.
A prototype AOE system was implemented to demonstrate the measurement of the strain response of hydrated chicken skeletal muscle to an applied dynamic acoustic stress. An electroacoustic transducer was placed in light contact with the tissue samples and driven in a sinusoidal waveform at 2 Hz by a function generator, launching acoustic waves into the tissues. A collimated, TE cooled, index-guided diode laser emitting at 809 nm sequentially illuminated a narrow stripe of tissue (~1 cm in length) immediately adjacent to the electroacoustic transducer through q s = " 45° . The backscattered speckle patterns from each illumination angle were observed with a linear array CCD camera (7.6 m m pitch) equipped with an f/2.8 telecentric lens. The misfocus distance, Lo = 0.15 m. The CCD camera acquired a 1-D image from each illumination angle at a rate of 25 Hz and stacked the sequential images from each illumination angle into 2-D arrays such that sample number (or time) is given along the ordinate and pixel number (or space) is given along the abscissa. Thus 2 (one from each illumination angle) "stacked-speckle histories"8 were acquired during the duration of the tests (Fig. 5).
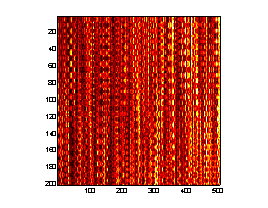
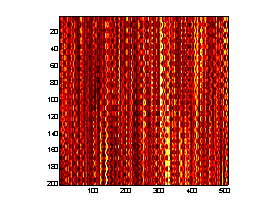
Figure 5. AOE stacked speckle histories.
The goal was to first estimate the shift as a function of record number and second to calculate the cumulative strains in the samples via the maximum likelihood approach and the instantaneous strain rates by taking the time derivative of Eq. (23).
Figure 6 shows the estimated speckle shift as a function of record number for Fig. 5. Figs. 7 and 8 show the cumulative strain as a function of record number and the instantaneous strain rate calculated via Eq. (23) and it's time derivative, respectfully. The gradual increase in cumulative strain shown in Fig. 7 implies that the tissue was creeping under the imposed dynamic acoustic stress, however this is a feature which requires further investigation.
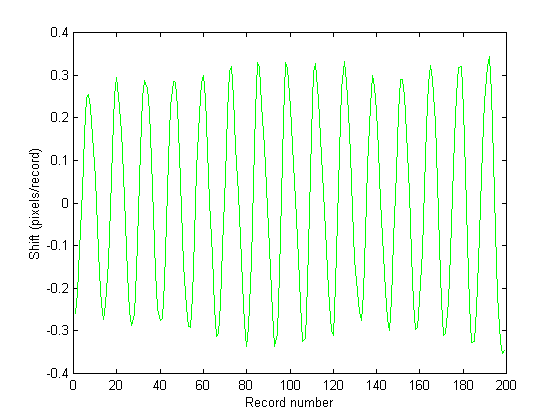
Figures 6 . Speckle shift in pixels/record as a function of record number. It can be seen that the speckle pattern does indeed shift in a sinusoidal manner, following the acoustic modulation. Figure 7 (bottom) shows the cumulative shift in the speckle pattern for the two illumination angles. The gradual separation in the direction of the shift for the two illumination angles indicates an increasing residual strain and/or rigid body motion.
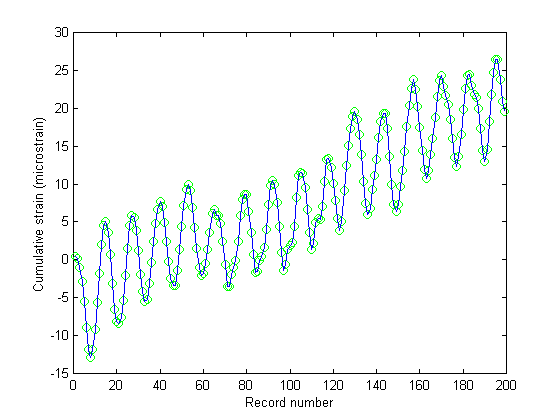
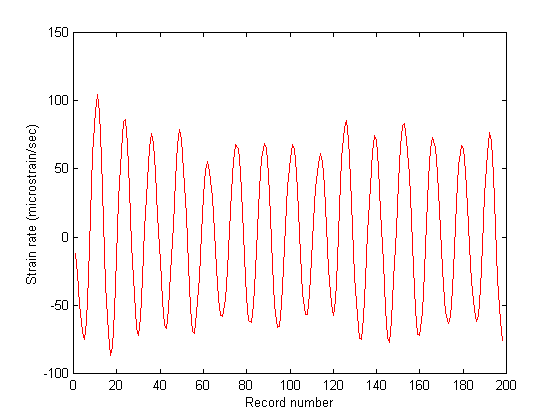
Figures 7 & 8. Figure 7 (top) shows the cumulative strain in the breast muscle as a function of record number. Apparently there was some residual strain that built-up due to the creep response of the tissue to the dynamic loading. This is a feature that may or may not be real, but warrants further investigation. Figure 8 (bottom) shows strain rate as a function of record number. As expected, the strain rate followed the sinusoidal acoustic loading pattern.
3. Discussion
In summary, these preliminary results demonstrate an imaging method by which acoustically induced speckle fluctuations in biological tissue can quantitatively encode mechanical information about the tissue. Pathological tissues, because their mechanical properties vary from that of healthy tissue, should exhibit a different strain response than will healthy tissues, which may assist in the early detection of cancerous lesions, for example. The system is noninvasive for superficial applications, such as the interrogation of skin. Alternatively, a minimally invasive, endoscope-based system can be envisioned for probing internal tissues, such as esophageal and prostate tissues.
4. Acknowledgements
I would like to thank Donald Duncan for extensive assistance during the course of this project. This work was funded in part by NSF grants #BES-9808497 and #BES-0086719.
5. References
1. R. Jones and C. Wykes, Holographic and Speckle Interferometry. A Discussion of the Theory, Practice and Applications of the Techniques, Cambridge University Press, Cambridge (1983).
2. K. J. Gåsvik, Optical Metrology Second Edition, John Wiley & Sons, Chichester (1995).
3. G. Cloud, Optical Methods of Engineering Analysis, Cambridge University Press, Cambridge (1995).
4. P. K. Rastogi (ed.), Optical Measurement Techniques and Applications, Artech House, Inc., Boston (1997).
5. A. Oulamara, G. Tribillon, and J. Duvernoy, "Biological activity measurement on botanical specimen surfaces using a temporal decorrelation effect of laser speckle," J. Mod. Opt., vol. 36, pp. 165-179 (1989).
6. R. M. Lerener, S. R. Huang, and K. J. Parker, "Sonoelasticity images derived from ultrasound signals in mechanically vibrated tissues," Ultrasound in Med & Biol., vol. 16, no. 3, pp. 231-239 (1990).
7. J. Ophir, I. Cespedes, H. Ponnekanti, Y. Yazdi, X. Li, "Elastography: A quantitative method for imaging the elasticity of biological tissues," Ultrason. Imaging, vol. 13, pp. 111-134 (1991).
8. H. E. Talhami, L. S. Wilson, and M. L. Neale, "Spectral tissue strain: a new technique for imaging tissue strain using intravascular ultrasound," Ultrasound in Med & Biol., vol. 20, no. 8, pp. 759-772 (1994).
9. R. Muthupillai, P. J. Rossman, D. J. Lomas, J. F. Greenleaf, S. J. Riederer, and R. L. Ehman, "Magnetic resonance imaging of transverse acoustic waves," MRM, vol. 36, pp. 266-274 (1996).
10. S. J. Kirkpatrick and M. J. Cipolla, "High resolution imaged laser speckle strain gauge for vascular applications," J. Biomed Optics, vol. 5, no. 1, pp. 62-71.
11. I. Yamaguchi, "Speckle displacement and decorrelation in the diffraction and image fields for small object deformation," Opt. Acta, vol. 28, pp. 1359-1376 (1981).
12. I. Yamaguchi, "Simplified laser speckle strain gauge," Opt. Eng., vol. 21, pp. 436-440 (1982).
13. I. Yamaguchi, "Advances in the laser speckle strain gauge," Opt. Eng., vol. 27, 214-218 (1988).
14. D. D. Duncan, F. F. Mark, and L. W. Hunter, "A new speckle technique for noncontact measurement of small creep rates," Opt. Eng., vol. 31, pp. 1583-1589 (1992).
15. D. D. Duncan, S. J. Kirkpatrick, F. F. Mark, and L. W. Hunter, "Transform method of processing for speckle strain-rate measurements," Appl. Opt., vol. 33, no. 22, pp. 5177-5186 (1994).
16. S. J. Kirkpatrick and B. W. Brooks, "Micromechanical behavior of cortical bone as inferred from laser speckle data," J. Biomed Mater Res, vol. 39, pp. 373-379 (1998).
17. M. C. Roggemann and B. Welsh, Imaging Through Turbulence, CRC Press, Boca Raton (1996).
18. A. D. Belegundu and T. R. Chandrupatla, Optimization Concepts and Applications in Engineering, Prentice Hall, Upper Saddle River, NJ (1999).
19. R. J. Shilling and S. L. Harris, Applied Numerical Methods for Engineers Using MATLAB and C, Brooks/Cole Pacific Grove (2000).
20. B. Jähne, Practical Handbook on Image Processing for Scientific Applications, CRC Press, Boca Raton (1997).
21. B. R. Frieden, Probability, Statistical Optics, and Data Testing: A Problem Solving Approach, Second Edition, Springer-Verlag, Berlin (1991).
22. H. L. Van Trees, Detection, Estimation, and Modulation Theory, Part I, John Wiley and Sons, New York (1968).