Diffuse reflectance from a semiinfinite medium

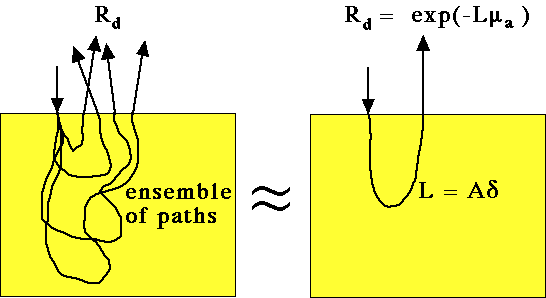
When photons enter a tissue, they scatter and escape out the surface where they are observable. The escaping flux of light is called "diffuse reflectance", R_d. The value of R_d depends on the absorption coefficient of the tissue, µ_a, and the effective pathlength L that photons travel in the tissue.

R_d is uniquely related to the ratio of scattering to absorption. The more scattering events that occur before the photon is absorbed, the more likely is the photon to be returned to the surface for escape as observable reflectance. If both the absorption and the reduced scattering coefficients are doubled or halved, the R_d does not change because the ratio of scattering to absorption remains constant.

The diffuse reflectance from the surface of a semi-infinite homogeneous medium with absorption coefficient µ_a [cm^-1] and reduced scattering coefficient coefficient µ_s' [cm^-1] is approximated by the expression:

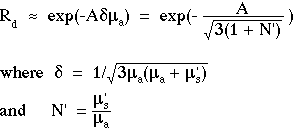
is the 1/e optical penetration depth. N' is defined as the ratio of reduced scattering to absorption. The factor A equals the apparent pathlength L for photon attenuation due to the absorption coefficient µ_a. In other words, the ensemble of photon pathlengths for escaping light observed as R_d can be approximated by a single pathlength L = A.

The following figure shows the behavior of R_d for an aqueous solution, in other words for a refractive index mismatch of 1.33:1 at the air/medium surface:

for air/water surface with refractive index mismatch 1.33:1.

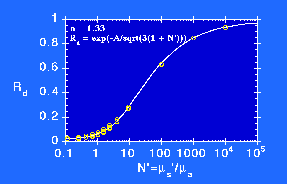
which is based on calculations using the Adding-Doubling Method. The data are for various choices of choices of absorption and reduced scattering and for various choices of anisotropy, g = 0, 0.5, 0.8, 0.9, 0.95. Above R_d = 0.40, g has no influence on R_d. Below R_d = 0.40, the R_d depends on the anisotropy.

The value of A is not constant, and depends on N' and the refractive index mismatch at the air/medium surface. The value of A is roughly about 7-8 for most soft tissues, and choosing a constant value of A allows Eq. 1 to roughly mimic the behavior of R_d. For an accurate calculation of R_d, however, the appropriate value of A should be specified as a function of N':

for air/water surface with refractive index mismatch 1.33:1.

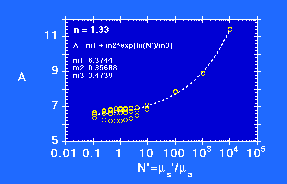
In summary, R_d is a function of µ_s'/µ_a = N'.

Deduce N' from a measurement of R_d

A measurement of R_d is perhaps the simplest measurement one can make on a semi-infinite scattering medium. The following figure illustrates how measurements on the unknown medium (M) and on a standard reflectance (M_std) whose reflectance is R_std yield R_d:

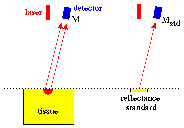
Once R_d is specified, one can calculate N':

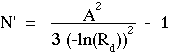
Since A is a function of N', one must use an iterative loop, or a fitting routine, to specify both A and N' from a given R_d. N' and A are not independent, so we are still specifying only one unknown, N', from one independent variable, R_d. A simple MATLAB program illustrates such an iterative loop: N' = findNp(Rd).