ECE532 Biomedical Optics © 1998 Steven L. Jacques, Scott A. Prahl Oregon Graduate Institute

Diffusion theory

Limits of diffusion theory

There are limits to the applicability of diffusion theory.

It is important to remember that diffusion theory simply attempts to mimic Fick's 1st law of diffusion by a proper choice of D to relate J and -dF/dr. The approximation of F(r) as simply a linear perturbation of the value F(0) neglects higher order terms that depend on d²F/dr². Sometimes the gradient has significant curvature within the spherical regime from which exp(-µ_s' r) allows photons to pass through the aperture. In such regions, the linear approximation to F(r) is inadequate and diffusion theory is inaccurate. Two cases of curvature deserve emphasis:

Near a source

The gradients are very steep near a point source or collection of point sources with both the exponential term exp(-r/(4cDt)) and the term 1/r causing significant curvature in the gradients. Distant from sources, gradients become gradual and diffusion theory is more accurate.

Absorption

Strong absorption prevents photons from engaging in an extended random walk. The approximation µ_t = µ_s' becomes inadequate. In common use is the approximation:

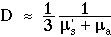
However, we have conducted Monte Carlo simulations of light diffusion from an isotropic point source to yield the spatial distribution for F(r) which suggests a different value for D:

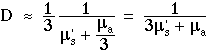
If µ_a << 3µ_s', the effect of absorption can be neglected.