ECE532 Biomedical Optics
© 1998 Steven L. Jacques, Scott A. Prahl
Oregon Graduate Institute

Angular patterns of Mie scattering

Consider the scattering pattern from a 0.304-µm-dia. nonabsorbing polystyrene sphere in water irradiated by HeNe laser beam:

n_p = 1.5721 particle refractive index
n_med = 1.3316 medium refractive index
a = 0.152 µm, particle radius
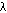= 0.6328 µm wavelength in vacuo

As calculated before:

n_r = n_p/n_med = 1.5721/1.3316 = 1.1806 relative refractive index
x = 2πa/(λ>/n_med) = (2)(3.1415)(0.152)/(0.6328/1.3316) = 2.0097 size parameter

Run the Mie theory algorithm:

Mie(n_r, x) ---> S₁(θ), S₁(θ) as complex numbers

Mie(1.1806, 2.0097) ---> S_1.re + jS_1.im, S_2.re + jS_2.im as functions of θ

To view the results, calculate the intensities of scattering for parallel and perpendicular orientations of polarized source/detector pairs:

I_par = S₂S₂^* = Re{(S_2.re + jS_2.im)(S_2.re - jS_2.im)}

I_per = S₁S₁^* = Re{(S_1.re + jS_1.im)(S_1.re - jS_1.im)}

which are shown in the following figures, and can be experimentally measured as described below.

The following figures describe the experimental measurements that illustrate the angular dependence of the scattered intensities I_par and I_per:

I_per

Irradiate dilute solution of spheres in water with laser beam polarization oriented perpendicular to the table. Collect scattered light as a function of angle θ in plane parallel to table. Place linear polarization filter in front of detector perpendicular to the table.

I_par

Irradiate dilute solution of spheres in water with laser beam polarization oriented parallel to the table. Collect scattered light as a function of angle θ in plane parallel to table. Place linear polarization filter in front of detector parallel to the table.

Example results: Polar and xy plots of scattering pattern for I_par and I_per

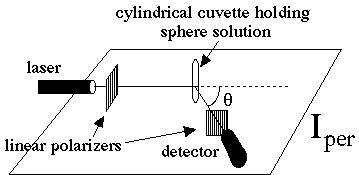
Polar plot

I(θ) plot

For a randomly polarized light source, the total scattered light intensity is given by the term S₁₁:

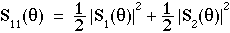
S₁₁ is the first element of the so-called Mueller Matrix, a 4x4 matrix which relates an input vector of Stokes parameters (I_i, Q_i, U_i, V_i) describing a complex light source and the output vector (I_s, Q_s, U_s, V_s) describing the nature of the transmitted light. For randomly polarized light, S₁₁ describes the transport of total intensity:

I_s = S₁₁I_i

next | Mie | Optical Properties

n_p = 1.5721	particle refractive index
n_med = 1.3316	medium refractive index
a = 0.152 µm,	particle radius
= 0.6328 µm	wavelength in vacuo

n_r = n_p/n_med = 1.5721/1.3316 = 1.1806	relative refractive index
x = 2πa/(λ>/n_med) = (2)(3.1415)(0.152)/(0.6328/1.3316) = 2.0097	size parameter

Angular patterns of Mie scattering

Run the Mie theory algorithm:

Iper

Ipar

Example results: Polar and xy plots of scattering pattern for Ipar and Iper

I_per

I_par

Example results: Polar and xy plots of scattering pattern for I_par and I_per