
© 1998 Steven L. Jacques, Scott A. Prahl
Oregon Graduate Institute

| ECE532 Biomedical Optics © 1998 Steven L. Jacques, Scott A. Prahl Oregon Graduate Institute |
L [W/(cm2 sr)]
| |
We now combine the concepts of Radiant Intensity and Irradiance in the parameter called the Radiance.
The Radiance L [W/(cm2 sr)] of a source equals the power P [W] that radiates from a surface within a solid angle Ω [sr] and passes through a cross-sectional area Acosθ [cm2], where θ is the angle between the direction of radiation and the normal to the surface A:
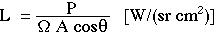
The radiance can also refer to a target area, describing the power per incremental solid angle irradiating an incremental cross-sectional area of target. The above definition strictly holds in the limit of very narrow solid angle (Ω -> 0) and very small surface area (A -> 0) to describe the radiance from a local region into a specific direction.
The following figures illustrate schematically the radiance of a source (left) and a target (right) for the case of θ = 0, i.e., the surface is perpendicular to the central direction of the cones of radiation. The figures attempt to schematically depict a continuous and uniform distribution of radiating cones, although graphically only some representative cones are shown.
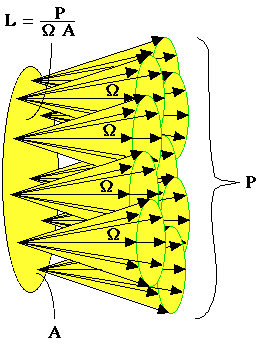 a source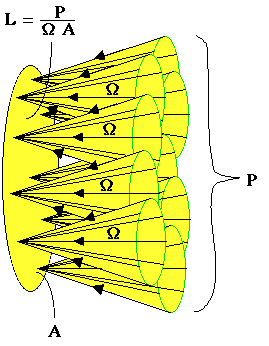 a target |
The following example emphasizes the radiance from a surface that is oriented oblique to the central direction of radiation. The surface is oriented at an angle θ relative to the central direction of radiation. The radiance L refers to the power passing through the area A but weighted by cosθ which equals the area shown in red, area Acosθ:
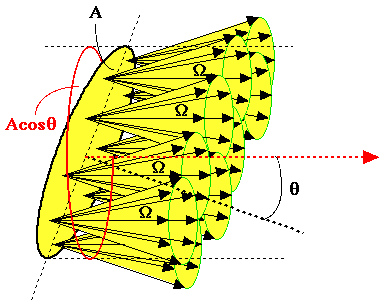
In the above schematic figure, you might get confused. How does all the power P go through the red circle? Graphically, it is not obvious. The answer is found in emphasizing that the definition of radiance is in the limit of a very narrow solid angle (Ω -> 0) and a very small surface area (A -> 0). The following figures schematically illustrate these two limiting cases:
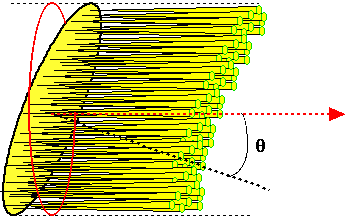 In limit of Ω -> 0 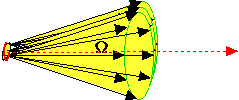 In limit of A -> 0 |
Hopefully you can see that in the limit of narrow solid angle and small area, the power does go through the red area Acosθ. It is common to express radiance by the differential expression:
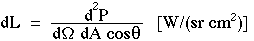
Example: | Radiance of a flashlight |
Next | Radiometry |